概率论与数理统计教程 茆诗松 第一、二章

补习基础数理知识之概率论

第一章 随机事件与概率

1.1 随机事件及其运算

1.1.1 随机现象

随机现象的两个特点：

• 结果不止一个
• 我们并不知道哪个结果会出现

1.1.2 样本空间

样本空间就是随机现象所有可能的结果组成的集合，根据其中元素的特点（是否可以全部列出、个数是否有限等）可以分为离散样本空间和连续样本空间

样本空间通常用 $\Omega$ 表示

1.1.3 随机事件

随机事件是样本空间的子集，即随机事件是一个集合，集合中的元素是随机现象部分或全部可能的结果

根据随机事件中包含随机现象结果个数的多少，可以将其分成以下几类：

• 基本事件：随机事件只包含随机现象的一个可能的结果
• 必然事件：随机事件包含随机现象的全部可能的结果
• 不可能事件：随机事件是空集（可以这样理解：随机事件是空集，也就是说集合中没有随机现象任何可能的结果，随机现象不会发生，此事件也就是不可能事件）

1.1.4 随机变量

用来表示随机现象结果的变量

1.1.6 事件间的运算

对立事件

事件$A$ 的对立事件记为 $\bar{A}$ ，是由在 $\Omega$ 中且不在 $A$ 中的样本点组成的新事件

注意，互为对立事件的两个事件的并集就是样本空间本身，即有

$$A \cup \bar{A} = \Omega\ ,A \cap \bar{A} = \varnothing$$

记录一个等式 $A-B=A\bar{B}$

互不相容事件

一个维恩图就能解释：

事件$A$与事件$B$虽然没有共同的样本点，但是它们的并集不是整个样本空间，这是它与对立事件最大的不同。

所以对立事件一定是互不相容事件，但互不相容事件不一定是对立事件。

对偶律（德摩根公式）

事件并的对立等于对立的交：$\overline{A \cup B}=\overline{A}\cap \overline{B}$

事件交的对立等于对立的并：$\overline{A \cap B}=\overline{A}\cup \overline{B}$

1.1.7 事件域

定义：设$\Omega$为一样本空间，$\mathscr{F}$为$\Omega$的某些子集所组成的集合类。如果 满足：

1. $\Omega\in \mathscr{F}$,
2. $A\in \mathscr{F}$,则对立事件$\overline{A}\in \mathscr{F}$,
3. 若$A_n\in \mathscr{F},n=1,2,\cdots$，则可列并$\bigcup_{n=1}^{\infty}A_n \in \mathscr{F}$.

则称$\mathscr{F}$为一个事件域，又称为$\sigma$域或$\sigma$代数。

在概率论中，称$(\Omega, \mathscr{F})$为可测空间，这里的可测是说$\mathscr{F}$中都是有概率可言的事件。既然$\mathscr{F}$中都是事件，那么就说明$\mathscr{F}$是由集合组成的，也就是说集合类中都是集合。

关于集合类的说明，引用知乎博主LEO LEO在文章概率论基础-01: 集合类中说的

由集合组成的大家庭就叫做集合类(也叫做 集类,集合系 set class, 集合里面装得都是一个又一个的集合).

习题1.1

1.写出下列随机试验的样本空间：

​ (1) 抛三枚硬币：{ (0, 0, 1), (0, 0, 0), (0, 1, 1), (1, 1, 1) }

​ (5) 口袋中有黑、白、红球各一个，从中不放回地任取两个球： { (黑, 白), (黑, 红), (白, 红) }

11.设$\mathscr{F}$为一事件域，若$A_n\in \mathscr{F},n=1,2,\cdots$，试证明：

​ （1）$\varnothing \in \mathscr{F}$;

​ 由事件域定义知，$\Omega \in \mathscr{F}$ 且 $\overline{\Omega} \in \mathscr{F}$，即 $\varnothing \in \mathscr{F}$

​ （2）有限并$\bigcup_{i=1}^{n}A_i \in \mathscr{F}, n\ge 1$;

​ 由事件域定义知可列并$\bigcup_{n=1}^{\infty}A_n \in \mathscr{F}$，令$A_i = \varnothing, i=n+1,\cdots,\infty$即可得$\bigcup_{i=1}^{n}A_i \in \mathscr{F}, n\ge 1$

​ （3）有限交$\bigcap_{i=1}^{n}A_i \in \mathscr{F}$;

​ $\bigcap_{i=1}^{n}A_i =\overline{\bigcup_{i=1}^{n}\overline{A_i}} \in \mathscr{F}$

​ （4）可列交$\bigcap_{i=1}^{\infty}A_i \in \mathscr{F}$;

​ $\bigcap_{i=1}^{\infty}A_i = \overline{\bigcup_{i=1}^{\infty}\overline{A_i}}\in \mathscr{F}$

​ （5）差运算$A_1-A_2\in \mathscr{F}$.

​ $A_1-A_2 = A\overline{A_2}\in \mathscr{F}$

作者就是想通过这个证明题告诉我们，事件域的定义给出了样本空间子集之间运算的所有可能结果。

1.2 概率的定义及其确定方法

1.2.1 概率的公理化定义

定义：设$\Omega$为一个样本空间， $\mathscr{F}$为$\Omega$的某些子集组成的一个事件域。如果对任一事件$A\in\mathscr{F}$，定义在 $\mathscr{F}$上的一个实值函数$P(A)$满足：

• 非负性公理 若$A\in\mathscr{F}$，则$P(A)\ge0$
• 正则性公理 $P(\Omega)=1$
• 可列可加性公理 若$A_1,A_2,\cdots,A_n,\cdots$互不相容，则

$$P(\bigcup_{i=1}^{\infty}A_i)=\sum_{i=1}^{\infty}P(A_i)$$

称$P(A)$为事件$A$的概率，称三元素$(\Omega,\mathscr{F},P)$为概率空间

1.2.2 排列与组合公式

以下排列组合公式的共同模型：从$n$个不同小球中取出$r$个

• 排列 $P_n^r=\frac{n!}{(n-r)!}$

• 重复排列 $n^r$

• 组合 $C_n^r=\frac{n!}{r!(n-r)!}$

• 重复组合 $C_{n+r-1}^{r}$

1.2.3 确定概率的频率方法

在$n$次重复试验中，记$n(A)$为事件$A$ 出现的次数或频数，

$$f_n(A)=\frac{n(A)}{n}$$

为事件$A$ 的频率

在试验次数$n$足够大时，事件的频率稳定在该事件的概率附近，频率是概率的一个近似。

1.2.4 确定概率的古典方法

古典方法基本思想如下：

• 涉及的随机现象只有有限个样本点，这里记为$n$个
• 每个样本点发生的可能性相等
• 如果事件 $A$ 含有$k$个样本点，那么事件$A$的概率为

$$P(A)=\frac{k}{n}$$

1.2.5 确定概率的几何方法

几何方法的基本思想：

• 如果一个随机现象的样本空间$\Omega$充满某个区域，其度量（长度、面积或体积等）大小可用$S_{\Omega}$表示
• 任意一点落在度量相同等子区域内是等可能的
• 如果事件$A$为$\Omega$中的某个子区域，其度量大小用$S_A$表示，则事件$A$的概率为

$$P(A)=\frac{S_A}{S_{\Omega}}$$

习题1.2

1.对于组合数$C_{n}^{r}$，证明：

​ （5）$C_{a}^{0}C_{b}^{n}+C_{a}^{1}C_{b}^{n-1}+\cdots+C_{a}^{n}C_{b}^{0}=C_{a+b}^{n}, n=min\{a,b\}$

​ 这一问考虑实际意义更加方便，从$a+b$个小球中取出$n$个小球，有多少种取法？

​ 等式左边是先从$a$个球中取$r$个，再从$b$个球中取$n-r$个球，等式右边是直接从所有球中取出$n$个。最终的取法数量是相等的

​ （6）${C_{n}^{0}}^2+{C_{n}^{1}}^2+\cdots+{C_{n}^{n}}^2=C_{2n}^{n}$

​ 第5问的一种特殊情况，即$a=b=n$，等式依然是成立的

16.（握草问题）一个人把六根草握在手中，仅仅露出它们的头和尾，然后随机地把六个头两两相接，六个尾也两两相接，求放开手后六根草恰巧连成一个环的概率。

样本空间内样本点个数为$(C_6^2C_4^2C_2^2)^2$

设事件$A$：放开手后六根草连成一个环

事件$A$的样本点数为$C_5^1C_4^1C_3^1C_2^1$

事件$A$的概率为

$$P(A)=\frac{C_5^1C_4^1C_3^1C_2^1}{(C_6^2C_4^2C_2^2)^2}=\frac{2}{135}$$

17.把$n$个0与$n$个1随机排列，求没有两个1连在一起的概率

我们首先把所有的0取出来，这个概率是$\frac{1}{C_{2n}^n}$

然后把所有的1放置在0中间，题目要求没有两个1连在一起，所以两个1之间必须有至少一个0，换句话说，就是把1放在0之间的空隙中。

$n$个0形成了$n+1$个空隙，放入$n$个1的可能方案有$C_{n+1}^n=n+1$种，所以概率为

$$P=\frac{C_{n+1}^n}{C_{2n}^{n}}=\frac{n+1}{C_{2n}^{n}}$$

1.3 概率的性质

性质1.3.1 $P(\varnothing)=0$

性质1.3.2 若有限个事件$A_1, A_2, \cdots, A_n$互不相容，则有

$$P(\bigcup_{i=1}^{n}A_i)=\sum_{i=1}^{n}P(A_i)$$

性质1.3.3 对任一事件$A$，有

$$P(\overline{A})=1-P(A)$$

性质1.3.4 若$A\supset B$，则$P(A-B)=P(A)-P(B)$

性质1.3.5 对任意两个事件$A$，$B$，有

$$P(A-B)=P(A)-P(AB)$$

性质1.3.6 对任意两个事件$A$，$B$，有

$$P(A\cup B)=P(A)+P(B)-P(AB)$$

对任意$n$个事件$A_1,A_2,\cdots,A_n$，有

$$\begin{aligned} P(\bigcup_{i=1}^{n}A_i)=&\sum_{i=1}^{n}P(A_i)-\sum_{1\le i \lt j \le n}{P(A_iA_j)}+\sum_{1\le i \lt j \lt k \le n}{P(A_iA_jA_k)}\\ &+\cdots +(-1)^{m-1}\sum_{1\le i_1 \lt i_2 \lt\cdots<i_m \le n}P(A_{i_1}A_{i_2}\cdots A_{i_m})\\ &+(-1)^{n-1}\sum{P(A_1A_2\cdots A_n)} \end{aligned}$$

1.3.4 概率的连续性

先不了解

习题1.3

14.某班$n$个战士各有1支归个人保管的枪，这些枪外形完全一样，在一次夜间紧急集合中，每个人随机地取了1支枪，求至少有一人拿到自己的枪的概率

设事件$A$：所有人都没有拿到自己的枪；事件$B$：至少有一人拿到自己的枪

$B=\overline{A}$

样本空间内样本点的个数为 $n(n-1)(n-2)\cdots1=n!$，所以现在的任务是求事件$A$的样本点的个数

所有人都没有拿到自己的枪可以转化为这样一个模型：把有带有标号$1,2,\cdots,n$的小球放入带有标号$1,2,\cdots,n$的盒子内，每个盒子内有且只有一个球，问有多少种完全错序的情况（即不存在球的标号与盒子标号相同的情况）

设$P_n$为有$n$个小球，$n$个盒子的完全错序数，容易求得$P_1=0,P_2=1,P_3=2,P_4=9$

手算$P_5$时就会觉得有点繁琐了，所以想寻找${P_n}$这个数列的递推公式，然后求解通项公式

首先放入标号为1的球，共有$n-1=4$种选择，假设放在第二个盒子里

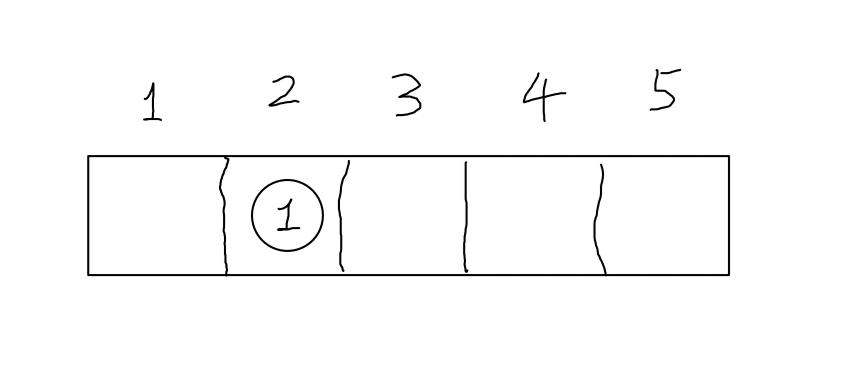
接着放标号为2的球，这里分为两种情况，

1.标号为2的球放在1号盒子里

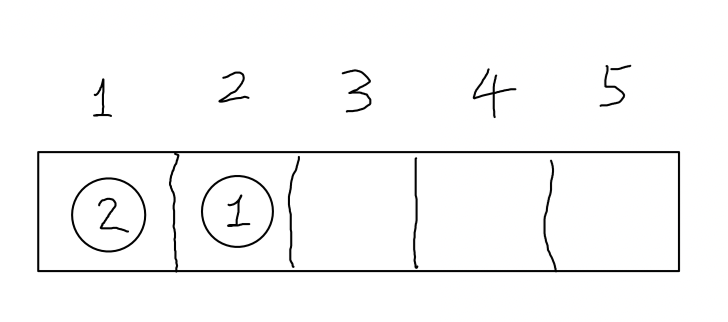
此时剩下标号为3，4，5的球要完全错序地放在3，4，5号盒子里，一共有$P_{5-2}=P_{3}$种放法

2.标号为2的球不放在标号为1的盒子里，此时有标号为2，3，4，5的球和标号为1，3，4，5的盒子，且2号球不放在一号盒子里，那么这里就可以把1号盒子想象成2号盒子（因为这个时候1号盒子起到了2号盒子的作用，即2号球不能放入这个盒子），相当于把2，3，4，5号球完全错序地放入2，3，4，5号盒子里，共有$P_{5-1}=P_4$种放法

综合上面两步，知道$P_5=(5-1)\times(P_{5-2}+P_{5-1})=4\times(2+9)=44$

由此得到递推公式$P_n=(n-1)(P_{n-1}+P_{n-2})$

求得通项公式为

$$P_n=\sum_{i=2}^{n}(-1)^i\frac{n!}{i!},\ n\ge2$$

所以

$$P(A)=\frac{P_n}{n!}=\sum_{i=2}^{n}(-1)^i\frac{1}{i!},\ n\ge2\\ P(B)=P(\overline{A})=1-P(A)=1-\sum_{i=2}^{n}(-1)^i\frac{1}{i!}=\sum_{i=1}^{n}(-1)^{i+1}\frac{1}{i!}$$

1.4 条件概率

1.4.1 条件概率的定义

条件概率是指在某事件$B$发生的条件下，求另一事件$A$的概率，记为$P(A|B)$

定义1.4.1 设$A$ 与 $B$是样本空间$\Omega$中的两个事件，如果$P(B)>0$，则称

$$P(A|B)=\frac{P(AB)}{P(B)}$$

为在$B$ 发生下$A$的条件概率

1.4.2 乘法公式

性质1.4.2 乘法公式

• 若$P(B)>0$，则

$$P(AB)=P(B)P(A|B)$$

• 若$P(A_1A_2\cdots A_{n-1})>0$，则

$$P(A_1A_2\cdots A_{n-1}A_n)=P(A_1)P(A_2|A_1)P(A_3|A_1A_2)\cdots P(A_n|A_1\cdots A_{n-1})$$

1.4.3 全概率公式

性质1.4.3 设$B_1, B_2,\cdots ,B_n$为样本空间$\Omega$的一个分割，即$B_1, B_2,\cdots ,B_n$互不相容，且$\bigcup_{i=1}^{n}B_i=\Omega$，如果$P(B_i)>0, i=1,2,\cdots,n$，则对任一事件$A$有

$$P(A)=\sum_{i=1}^{n}P(B_i)P(A|B_i)$$

1.4.4 贝叶斯公式

性质1.4.4 设$B_1,B_2,\cdots,B_n$是样本空间$\Omega$的一个分割，如果$P(A)>0,P(B_i)>0,i=1,2,\cdots,n$，则

$$P(B_i|A)=\frac{P(AB_i)}{P(A)}=\frac{P(B_i)P(A|B_i)}{\sum_{j=1}^{n}P(B_j)P(A|B_j)}$$

习题1.4

15.钥匙掉了，掉在宿舍里、掉在教室里、掉在路上的概率分别为50%、30%和20%，而掉在上述三处地方被找到的概率分别是0.8、0.3和0.1。试求找到钥匙的概率。

设事件$A$为找到钥匙，事件$B_i,i=1,2,3$分别为钥匙掉在宿舍里、掉在教室里、掉在路上，则

$$P(A)=\sum_{i=1}^{3}P(B_i)P(A|B_i)=0.5\times0.8+0.3\times0.3+0.2\times0.1=0.51$$

21.将$n$根绳子的$2n$个头两两相接，求恰好接成$n$个圈的概率

接成$n$个圈只有一种可能，即每条绳子自己的头尾相接

$$P=\frac{1}{\prod_{i=2}^{2n}C_i^2}$$

33.若$P(A|B)=1$，证明：$P(\overline{B}|\overline{A})=1$

$P(\overline{A}|B)=1-P(A|B)=0$

$$P(\overline{B}|\overline{A})=\frac{P(\overline{A}|\overline{B})P(\overline{B})}{P(\overline{A}|\overline{B})P(\overline{B})+P(\overline{A}|{B})P({B})}=\frac{P(\overline{A}|\overline{B})P(\overline{B})}{P(\overline{A}|\overline{B})P(\overline{B})}=1$$

1.5 独立性

1.5.1 两个事件的独立性

两个事件之间的独立性：一个事件的发生不影响另一个事件的发生

定义 如果有$P(AB)=P(A)P(B)$，则称事件$A$ 与$B$相互独立，简称$A$ 与$B$独立。否则$A$ 与$B$不独立。

性质1.5.1 若事件$A$ 与$B$独立，则$\overline{A}$ 与$B$独立，$A$ 与$\overline{B}$独立，$\overline{A}$ 与$\overline{B}$独立。

1.5.2 多个事件的相互独立性

定义 设有$n$个事件$A_1,A_2,\cdots,A_n$，对任意的$1\le i < j < k < \cdots \le n$，如果以下等式均成立

$$\begin{cases} \begin{aligned} P(A_i&A_j)=P(A_i)P(A_j),\\ P(A_i&A_jA_k)=P(A_i)P(A_j)P(A_k),\\ &\vdots\\ P(A_i&A_j\cdots A_n)=P(A_i)P(A_j)\cdots P(A_n)\\ \end{aligned} \end{cases}$$

则称这$n$个事件$A_1,A_2,\cdots,A_n$相互独立。

1.5.3 试验的独立性

定义 设有两个试验$E_1$ 和$E_2$，假如试验$E_1$的任一结果（事件）与试验$E_2$的任一结果（事件）都是相互独立的事件，则称这两个试验相互独立。

$n$重独立重复试验：$n$个相同的独立试验

$n$重伯努利试验：每次试验结果只有两个：$A$和 $\overline{A}$ 的$n$重独立重复试验（比如抛$n$次硬币）

第二章 随机变量及其分布

2.1 随机变量及其分布

2.1.1 随机变量的概念

定义 定义在样本空间上$\Omega$上的实值函数$X=X(\omega)$称为随机变量，随机变量常用大写字母$X,Y,Z$等表示，其取值用小写字母$x,y,z$等表示。假如一个随机变量仅可能取有限个或可列个值，则称其为离散随机变量。假如一个随机变量的可能取值充满数轴上的一个区间 $(a,b)$，则称其为连续随机变量，其中$a$ 可以是$-\infty$， $b$可以是 $\infty$

从定义中我们可以知道，所谓随机变量就是样本空间中样本点$\omega$的函数，利用随机变量将形式多样的样本点映射为数值，便于我们研究它。

2.1.2 随机变量的分布函数

定义 设$X$是一个随机变量，对任意实数$x$，称

$$F(x)=P(X\le x)$$

为随机变量$X$的分布函数。且称$X$服从$F(x)$，记为$X\sim F(x)$

定理 任一分布函数$F(x)$都具有如下三条基本性质：

• 单调性 $x_1<x_2 , F(x_1)\le F(x_2)$
• 有界性 对任意$x$，有$0\le F(x) \le 1$
• 右连续性 $\lim_{x \to x_0^+}F(x)=F(x_0) $

2.1.3 离散随机变量的概率分布列

定义 设$X$是一个离散随机变量，如果$X$的所有可能取值是$x_1,x_2,\cdots ,x_n,\cdots ,$ 则称$X$取$x_i$的概率

$$p_i = p(x_i) = P(X=x_i),\ i=1,2,\cdots ,n,\cdots$$

为$X$的概率分布列或分布列，记为$X\sim \{p_i\}$

2.1.4 连续随机变量的概率密度函数

首先要指明的是，概率密度函数$p(x)$在某一点$x$的取值不是随机变量取$x$的概率

类比密度$\rho$，它需要乘以对应的度量（体积$v$）才能得到质量$m$

概率密度函数也需要乘以对应的度量（$x$轴上的一个微元$dx$）才能得到概率，具体来说

$$p(x)dx\approx P(x<X<x+dx)\\ \int_a^bp(x)dx=P(a<X<b)\\$$

特别地，

$$\int_{-\infty}^{x}p(x)dx=F(x)$$

定义 设随机变量$X$的分布函数为$F(x)$，如果存在实数轴上的一个非负可积函数$p(x)$，使得对任意实数$x$有

$$F(x)=\int_{-\infty}^{x}p(t)dt$$

则称$p(x)$为$X$的概率密度函数，或称密度函数，或称密度。

习题 2.1

1.口袋中有5个球，编号为1，2，3，4，5，从中任意取3个，以$X$表示取出的3个球中最大的号码。（1）求$X$的分布列；（2）写出$X$的分布函数。

$X$可能的取值有3，4，5，相应的概率可以用古典方法求解：

$P(X=3)=\frac{C_2^2}{C_5^3}=\frac{1}{10}$

$P(X=4)=\frac{C_3^2}{C_5^3}=\frac{3}{10}$

$P(X=5)=\frac{C_4^2}{C_5^3}=\frac{3}{5}$

$X$的分布函数：

$$F(x)= \begin{cases} \begin{aligned} 0&,\ x<3\\ \frac{1}{10}&, \ 3\le x < 4\\ \frac{2}{5}&, \ 4 \le x <5\\ 1&, \ x \ge 5 \end{aligned} \end{cases}$$

15.设连续随机变量$X$的分布函数为

$$F(x)= \begin{cases} \begin{aligned} 0,&\ x<0,\\ Ax^2,&\ 0\le x <1,\\\ 1,&\ x\ge1 \end{aligned} \end{cases}$$

求：（1）A；（2）$P(0.3<X<0.7)$；（3）$X$的密度函数。

$1=F(1)=\lim_{x \to {1-0}}Ax^2=A$ 所以$A=1$

$P(0.3<X<0.7)=F(0.7)-F(0.3)=0.49-0.09=0.4$

概率密度函数：

$$p(x)= \begin{cases} \begin{aligned} 0&,\ x<0,\\ 2x&,\ 0\le x <1,\\ 0&,\ x\ge 1 \end{aligned} \end{cases}$$

2.2 随机变量的数学期望

2.2.2 数学期望的定义

定义 设离散随机变量$X$的分布列为

$$p(x_i)=P(X=x_i),\ i=1,2,\cdots ,n,\cdots$$

如果

$$\sum_{i=1}^{\infty}|x_i|p(x_i)<\infty,$$

则称

$$E(X)=\sum_{i=1}^{\infty}x_ip(x_i)$$

为随机变量$X$的数学期望，简称期望或均值。

定义 设连续随机变量$X$的密度函数为$p(x)$。如果

$$\int_{-\infty}^{\infty}|x|p(x)dx<\infty,$$

则称

$$E(X)=\int_{-\infty}^{\infty}xp(x)dx$$

为随机变量$X$的数学期望，简称期望或均值。

2.2.3 数学期望的性质

定理 若随机变量$X$的分布用分布列$p(x_i)$或用密度函数$p(x)$表示，则$X$的某一函数$g(X)$的数学期望为

$$E[g(X)]= \begin{cases} \begin{aligned} \sum_{i}g(x_i)p(x_i),\ 离散场合\\ \int_{-\infty}^{\infty}g(x)p(x)dx,\ 连续场合 \end{aligned} \end{cases}$$

几条性质

• 若$c$是常数，则$E(c)=c$
• 对任意常数$a$，有$E(aX)=aE(X)$
• 对任意两个函数$g_1(x)$ 和$g_2(x)$，有

$$E(g_1(x)\pm g_2(x))=E(g_1(x) )\pm E(g_2(x))$$

习题 2.2

1.设离散型随机变量$X$的分布列为

$X$	-2	0	2
$P$	0.4	0.3	0.3

求$E(X), E(3X+5)$

$$E(X)=\sum x_ip(x_i)=-2\times0.4+0\times0.3+2\times0.3=-0.2 \\ E(3X+5) = 3E(X)+5=-0.2\times3+5=4.4$$

18.设随机变量$X$的密度函数为

$$p(x)= \begin{cases} \begin{aligned} \frac{3}{8}x^2&,\ 0<x<2,\\ 0&,\ 其他 \end{aligned} \end{cases}$$

求$\frac{1}{X^2}$的数学期望

$$E(\frac{1}{X^2})=\int_{0}^{2}\frac{1}{x^2}\frac{3}{8}x^2dx=\frac{3}{8}\times2=\frac{3}{4}$$

2.3 随机变量的方差与标准差

随机变量$X$的数学期望$E(X)$是分布的一种位置特征数，它刻画了$X$的取值总在$E(X)$周围波动。但这个位置特征数无法反映出随机变量取值的“波动”大小。

2.3.1 方差与标准差的定义

定义 如果随机变量$X^2$的数学期望$E(X^2)$存在，则称偏差平方$(X-E(X))^2$的数学期望$E((X-E(X))^2)$为随机变量$X$的方差，记为

$$Var(X)=E((X-E(X))^2)= \begin{cases} \begin{aligned} \sum_{i}(x_i-E(X))^2p(x_i),\ 离散场合\\ \int_{-\infty}^{\infty}(x-E(X))^2p(x)dx,\ 连续场合 \end{aligned} \end{cases}$$

称$\sqrt{Var(X)}$为随机变量$X$的标准差，记为$\sigma(X)$或$\sigma_X$

2.3.2 方差的性质

性质 $Var(X)=E(X^2)-(E(X))^2$

性质 常数的方差为0，即$Var(c)=0$，$c$为常数

性质 若$a,b$为常数，则$Var(aX+b)=a^2Var(X)$

2.3.3 切比雪夫不等式

定理 设随机变量$X$的数学期望和方差都存在，则对任意常数$\varepsilon >0$，有

$$P(|X-E(X)|\ge \varepsilon)\le \frac{Var(X)}{\varepsilon^2}$$

习题2.3

1.设随机变量$X$满足$E(X)=Var(X)=\lambda$，已知$E[(X-1)(X-2)]=1$，试求$\lambda$

$$Var(X)=E(X^2)-E(X)^2\Rightarrow E(X^2)=E(X)^2+E(X)\\ \begin{aligned} E[(X-1)(X-2)]=&E(X^2-3X+2)=E(X^2)-3E(X)+2\\ =&E(X)^2-2E(X)+2\\ =&1\\ \end{aligned} \\ \lambda^2-2\lambda+1=0\Rightarrow\lambda=1$$

8.设随机变量$X$的分布函数为

$$F(x)=1-e^{-x^2},\ x>0$$

试求$E(X)$和$Var(X)$

概率密度函数

$$p(x)= \begin{cases} \begin{aligned} 0,\ x\le 0,\\ 2xe^{-x^2},\ x>0. \end{aligned} \end{cases}$$

$E(X)=\int_{0}^{\infty}2x^2e^{-x^2}dx=\frac{\sqrt{\pi}}{2}$ 关键词高斯积分，记住积分式$\int_{0}^{\infty}e^{-x^2}dx=\frac{\sqrt{\pi}}{2}$

$E(X^2)=\int_{0}^{\infty}2x^3e^{-x^2}dx=1$

$Var(X)=E(X^2)-E(X)^2=1-\frac{\pi}{4}$

2.4 常用离散分布

2.4.1 二项分布

二项分布 $X\sim b(n,p)$

$$P(X=k)=C_{n}^{k}p^k(1-p)^{n-k}$$

期望和方差

$$\begin{aligned} E(X)=&\ \sum_{k=0}^{n}kC_{n}^{k}p^k(1-p)^{n-k}\\ =&\ n\sum_{k=1}^{n}C_{n-1}^{k-1}p^k(1-p)^{n-k}\\ =&\ np\sum_{k=1}^{n}C_{n-1}^{k-1}p^{k-1}(1-p)^{(n-1)-(k-1)}\\ =&\ np \end{aligned}$$

$E(X^2)=n(n-1)p^2+np$

$Var(X)=E(X^2)-E(X)^2=n(n-1)p^2+np-(np)^2=np(1-p)$

2.4.2 泊松分布

泊松分布 $X\sim P(\lambda)$

$$P(X=k)=\frac{\lambda^k}{k!}e^{-\lambda},\ k=0,1,2,\cdots, \lambda>0$$

期望和方差

$E(X)=\lambda, Var(X)=\lambda$

泊松分布的期望和方差都是参数$\lambda$的值

泊松定理 在$n$重伯努利试验中，记事件$A$在一次试验中发生的概率为$p_n$（与试验次数$n$有关），如果当$n\to \infty$时，有$np_n\to \lambda$，则

$$\lim_{n\to \infty}C_{n}^{k}p_n^k(1-p_n)^{n-k}=\frac{\lambda^k}{k!}e^{-\lambda}$$

由于泊松定理是在$np_n\to \lambda$条件下获得的，故在计算二项分布$b(n,p)$时，当$n$很大，$p$很小，而乘积$\lambda=np$大小适中时，可以用泊松分布作近似

2.4.3 超几何分布

超几何分布 $X\sim h(n,N,M)$

$$P(X=k)=\frac{C_{M}^{k}C_{N-M}^{n-k}}{C_{N}^{n}},k=0,1,\cdots,r,\ r=\min\{M,n\},\ M\le N,\ n\le N$$

超几何分布可以用来描述不放回抽样

期望和方差

$E(X)=n\frac{M}{N}, Var(X)=\frac{nM(N-M)(N-n)}{N^2(N-1)}$

2.4.4 几何分布与负二项分布

一、几何分布 $X\sim Ge(p)$

$$P(X=k)=(1-p)^{k-1}p,\ k=1,2,\cdots$$

期望和方差

$E(X)=\frac{1}{p}, Var(X)=\frac{1-p}{p^2}$

几何分布的无记忆性

设$X\sim Ge(p)$，则对任意正整数$m$与$n$有

$$P(X>m+n|X>m)=P(X>n)$$

二、负二项分布（巴斯卡分布）

在伯努利试验序列中，记每次试验中事件$A$发生的概率为$p$，如果$X$为事件$A$第$r$次出现时的试验次数，则$X$的可能取值为$r,r+1,\cdots,r+m,\cdots$。称$X$服从负二项分布或巴斯卡分布

$$P(X=k)=C_{k-1}^{r-1}p^{r}(1-p)^{k-r},\ k=r,r+1,\cdots$$

记为$X\sim Nb(r,p)$

期望和方差

$E(X)=\frac{r}{p}, Var(X)=\frac{r(1-p)}{p^2}$

习题 2.4

3.某优秀射手命中10环的概率为0.7，命中9环的概率为0.3.求该射手三次射击所得的环数不少于29环的概率

设随机变量$X$: 命中10环的次数

$X\sim b(3,0.7)$

$$\begin{aligned} P(X=2)+P(X=3)=&\ C_{3}^{2}0.7^2(1-0.7)^1+C_{3}^{3}0.7^3(1-0.7)^0\\ =&\ 3\times 0.49 \times 0.3+0.343=0.784 \end{aligned}$$

8.设$X$服从泊松分布，且已知$P(X=1)=P(X=2)$，求$P(X=4)$

$P(X=1)=\lambda e^{-\lambda}=\frac{\lambda^2}{2!}e^{-\lambda}=P(X=2)\Rightarrow \lambda=2$

$P(X=4)=\frac{2^4}{4!}e^{-2}=0.09$

2.5 常用连续分布

2.5.1 正态分布

一、密度函数和分布函数

$X\sim N(\mu,\sigma^2)$

$$p(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}},-\infty<x<\infty$$

$\mu$为位置参数，$\sigma$为尺度参数

$N(0,1)$称为标准正态分布

期望和方差

$E(X)=\mu, Var(X)=\sigma^2$

正态分布的$3\sigma$原则

设随机变量$X\sim N(\mu,\sigma^2)$，则

$$\begin{aligned} P(|X-\mu|<k\sigma)&=\Phi(k)-\Phi(-k)\\ &=2\Phi(k)-1\\ &= \begin{cases} 0.6826,\ k=1,\\ 0.9545,\ k=2,\\ 0.9973,\ k=3. \end{cases} \end{aligned}$$

可见，随机变量99.73%的值落在$(\mu-3\sigma,\mu+3\sigma)$内

2.5.2 均匀分布

均匀分布 $X\sim U(a,b)$

$$p(x)= \begin{cases} \displaystyle \frac{1}{b-a},\ a<x<b,\\ \displaystyle 0,\ 其他. \end{cases}\\ \\ F(x)= \begin{cases} 0,\ x<a,\\ \displaystyle \frac{x-a}{b-a},\ a\le x<b,\\ 1,\ x\ge b. \end{cases}$$

期望和方差

$E(X)=\displaystyle \frac{a+b}{2}, Var(X)=\displaystyle \frac{(b-a)^2}{12}$

2.5.3 指数分布

指数分布 $X\sim Exp(\lambda)$

$$p(x)= \begin{cases} \displaystyle \lambda e^{-\lambda x},\ x\ge 0,\\ \displaystyle 0,\ x \lt 0. \end{cases}\\ \\ F(x)= \begin{cases} 1-e^{-\lambda x},\ x\ge 0,\\ 0,\ x\lt 0. \end{cases}$$

期望和方差

$E(X)=\displaystyle \frac{1}{\lambda}, Var(X)=\displaystyle \frac{1}{\lambda ^2}$

指数分布的无记忆性

如果随机变量$X\sim Exp(\lambda)$，则对任意$s>0,t>0$，有

$$P(X>s+t|X>s)=P(X>t)$$

2.5.4 伽马分布

伽马函数

$$\Gamma(\alpha)=\int_0^\infty x^{\alpha-1}e^{-x}dx$$

伽马函数的性质：

• $\Gamma (1)=1,\Gamma (\displaystyle \frac{1}{2})=\sqrt{\pi}$

• $\Gamma(\alpha +1)=\alpha \Gamma(\alpha)$，如果$\alpha$为自然数$n$，有$\Gamma(n +1)=n \Gamma(n)=n!$

伽马分布 $X\sim Ga(\alpha,\lambda), \alpha>0, \lambda>0$

$$p(x)= \begin{cases} \displaystyle \frac{\lambda ^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\lambda x},\ x\ge0,\\ 0,\ x<0. \end{cases}$$

$\lambda$固定，$\alpha$取不同值时伽马分布密度函数的图像：

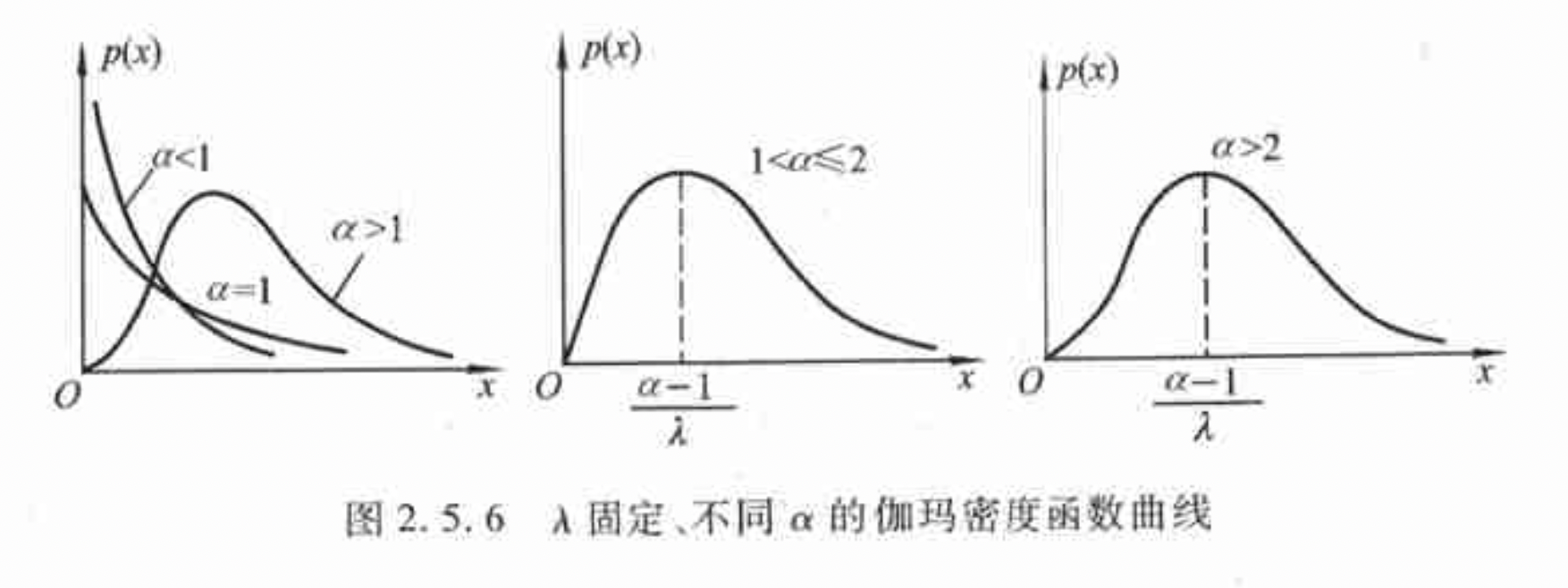
期望和方差

$E(X)=\displaystyle \frac{\alpha}{\lambda}, Var(X)=\displaystyle \frac{\alpha}{\lambda ^2}$

2.5.5 贝塔分布

贝塔函数

$$B(a,b)=\int_{0}^{1}x^{a-1}(1-x)^{b-1}dx,\ a>0,b>0.$$

贝塔函数的性质：

• $B(a,b)=B(b,a)$
• $\displaystyle B(a,b)=\frac{\Gamma(a) \Gamma(b)}{\Gamma(a+b)}$

贝塔分布 $X\sim Be(a,b)$

$$p(x)= \begin{cases} \displaystyle \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}x^{a-1}(1-x)^{b-1},\ 0<x<1,\\ 0,\ 其他. \end{cases}$$

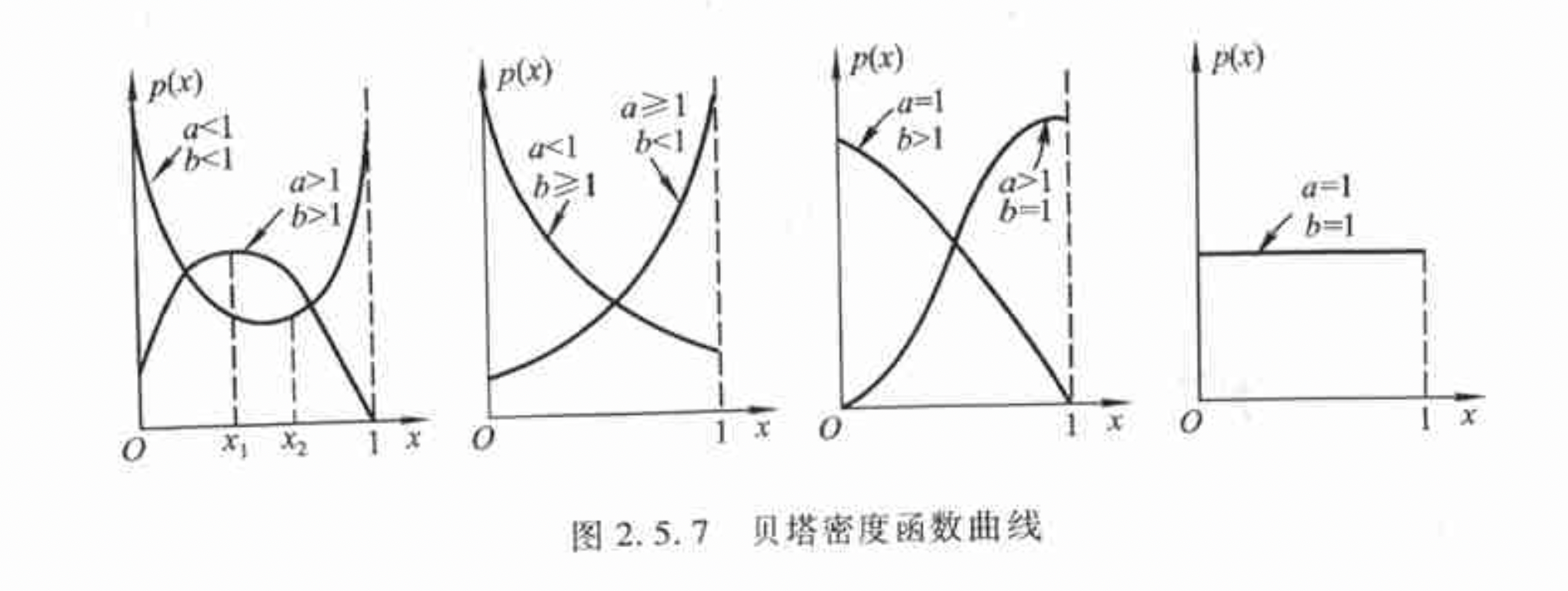
期望和方差

$E(X)=\displaystyle \frac{a}{a+b}, Var(X)=\displaystyle \frac{ab}{(a+b)^2(a+b+1)}$

习题2.5

1.设随机变量$X$服从区间$(2,5)$上的均匀分布，求对$X$进行3次独立观测中，至少有两次观测值大于3的概率

$\displaystyle P(X>3)=1-P(X\le 3)=1-\frac{3-2}{5-2}=\frac{2}{3}$

设随机变量$Y$：观测试验中，观测值大于3的次数

则$Y\sim b(3,\displaystyle \frac{2}{3})$

$\displaystyle P(Y\ge 2)=P(Y=2)+P(Y=3)=C_{3}^{2}(\frac{2}{3})^2\frac{1}{3}+C_{3}^{3}(\frac{2}{3})^3=\frac{4}{9}+\frac{8}{27}=\frac{20}{27}$

8.统计调查表明，英格兰1875年至1951年期间在矿山发生10人或10人以上死亡的两次事故之间的时间$T$服从均值为241的指数分布。求$P(50<T<100)$

$\displaystyle \frac{1}{\lambda}=241\Rightarrow \lambda = \frac{1}{241}$

$\displaystyle P(50<T<100)=F(100)-F(50)=1-e^{-\frac{1}{241} 100}-(1-e^{-\frac{1}{241} 50})=0.1523$

11.设顾客在某银行的窗口等待服务的时间$X$（以分钟计）服从指数分布，其密度函数为

$$p(x)= \begin{cases} \displaystyle \frac{1}{5}e^{-\frac{x}{5}},\ x>0,\\ 0,\ 其他. \end{cases}$$

某顾客在窗口等待服务，若超过10min他就离开。他一个月要到银行5次，以$Y$表示一个月内他未等到服务而离开窗口的次数，求$P(Y\ge 1)$

$P(X\gt 10)=\displaystyle\int_{10}^{\infty}\displaystyle \frac{1}{5}e^{-\frac{x}{5}}dx=e^{-2}$

$Y\sim b(5,e^{-2})$

$P(Y=0)=\textstyle C_{5}^{0}(1-e^{-2})^5=0.4833$

$P(Y\ge 1)=1-P(Y=0)=1-0.4833=0.5167$

25.设随机变量$X$服从正态分布$N(60,3^2)$，求实数$a,b,c,d$使得$X$落在如下五个区间中的概率之比为$7:24:38:24:7$

$$(-\infty,a],\ \ (a,b],\ \ (b,c],\ \ (c,d],\ \ (d,\infty)$$

$\displaystyle \frac{X-60}{3}\sim N(0,1)$

$P(\displaystyle \frac{X-60}{3}\le \displaystyle \frac{a-60}{3})=\Phi(\displaystyle \frac{a-60}{3})=0.07\Rightarrow\Phi(\displaystyle -\frac{a-60}{3})=0.93$

查表得到$a=55.56$，由对称性立即可得$d=64.44$

$P(\displaystyle \frac{X-60}{3}\le \displaystyle \frac{b-60}{3})=\Phi(\displaystyle \frac{b-60}{3})=0.31\Rightarrow\Phi(\displaystyle -\frac{b-60}{3})=0.69$

查表得到$b=58.5$，由对称性立即可得$c=61.5$

2.6 随机变量函数的分布

2.6.2 连续随机变量函数的分布

已知随机变量$X$的分布，求$Y=g(X)$的分布

一、$g(x)$严格单调

此时有定理 设$X$是连续随机变量，其密度函数为$p_X(x)$。$Y=g(X)$是另一个随机变量。若$y=g(x)$严格单调，其反函数$h(y)$有连续导数，则$Y=g(X)$的密度函数为

$$p(y)= \begin{cases} \displaystyle p_X[h(y)]|h^{'}(y)|,\ a<y<b,\\ 0,\ 其他. \end{cases}$$

$a=min({g(-\infty),g(\infty)}), b=max({g(-\infty),g(\infty)})$

定理 设随机变量$X$服从正态分布$N(\mu,\sigma^2)$，则当$a\ne 0$时，有$Y=aX+b \sim N(a\mu +b,a^2\sigma^2)$

定理（对数正态分布）设随机变量$X$服从正态分布$N(\mu,\sigma^2)$，则$Y=e^X$的概率密度函数为

$$p_Y(y)= \begin{cases} \displaystyle \frac{1}{\sqrt{2\pi}y\sigma}exp\{-\frac{(\ln y-\mu)^2}{2\sigma^2}\},\ y>0 \\ 0,\ y\le 0. \end{cases}$$

$Y\sim LN(\mu,\sigma^2)$

定理 设随机变量$X$服从伽马分布$Ga(\alpha,\lambda)$，则当$k>0$时，有$Y=kX\sim Ga(\alpha,\lambda /k)$

定理 若随机变量$X$当分布函数$F_X(x)$为严格单调增的连续函数，其反函数$F_X^{-1}(y)$存在，则$Y=F_X(X)$服从$(0,1)$上的均匀分布$U(0,1)$

2.7 分布的其他特征数

2.7.1 $k$阶矩

定义 设$X$为随机变量，$k$为正整数，如果以下数学期望都存在，则称

$$\mu_k=E(X^k)$$

为$X$的$k$阶原点矩。称

$$\nu_k=E[(X-E(X))^k]$$

为$X$的$k$阶中心矩。

对于$k$阶矩的理解，引用百度网友在这里的回答:

用“数学”语言通俗描述，$k$阶原点矩是随机变量$X$“偏离”原点$(0,0)$的“距离”的$k$次方的期望值。一般地，对于正整数$k$，如果$E|(X-0)^k|=E|X^k|<∞$，故称$E(X^k)$ 为随机变量$X$的$k$阶原点矩。$k$阶中心矩是随机变量$X$“偏离”其中心的“距离”的$k$次方的期望值。一般均以其平均数为“中心”。故，对于正整数$k$，如果$E(X)$存在，“偏离”$E(x)$距离的$k$次方的期望值存在、且$E[|X - E(X)|^k]<∞$，则称$E\{[X-E(X)]^k\}$为随机变量$X$的$k$阶中心矩。如$X$的方差是$X$的二阶中心矩，即$D(X)=E\{[X-E(X)]^2\}$ 等。

2.7.2 变异系数

设随机变量$X$的二阶矩存在，则称比值

$$C_\nu(X)=\frac{\sqrt{Var(X)}}{E(X)}=\frac{\sigma(X)}{E(X)}$$

为$X$的变异系数。

2.7.3 分位数

定义 设连续随机变量$X$的分布函数为$F(x)$，密度函数为$p(x)$。对任意$p\in (0,1)$，称满足条件

$$F(x_p)=\int_{-\infty}^{x_{p}}p(x)dx=p$$

的$x_p$为此分布的$p$分位数，又称下侧$p$分位数。

2.7.4 中位数

定义 设连续随机变量$X$的分布函数为$F(x)$，密度函数为$p(x)$。称$p=0.5$时的$p$分位数$x_{0.5}$为此分布的中位数，$x_{0.5}$满足条件

$$F(x_{0.5})=\int_{-\infty}^{x_{0.5}}p(x)dx=0.5$$

2.7.5 偏度系数

定义 设随机变量 $X$ 的前三阶矩存在，则如下比值

$$\beta_S=\frac{\nu_3}{\nu_{2}^{\frac{3}{2}}}=\frac{E\{[X-E(X)]^3\}}{[Var(X)]^{\frac{3}{2}}}$$

称为此分布的偏度系数，或称偏度。$\beta_S>0$，分布正偏，右偏； $\beta_S<0$，分布负偏，左偏。

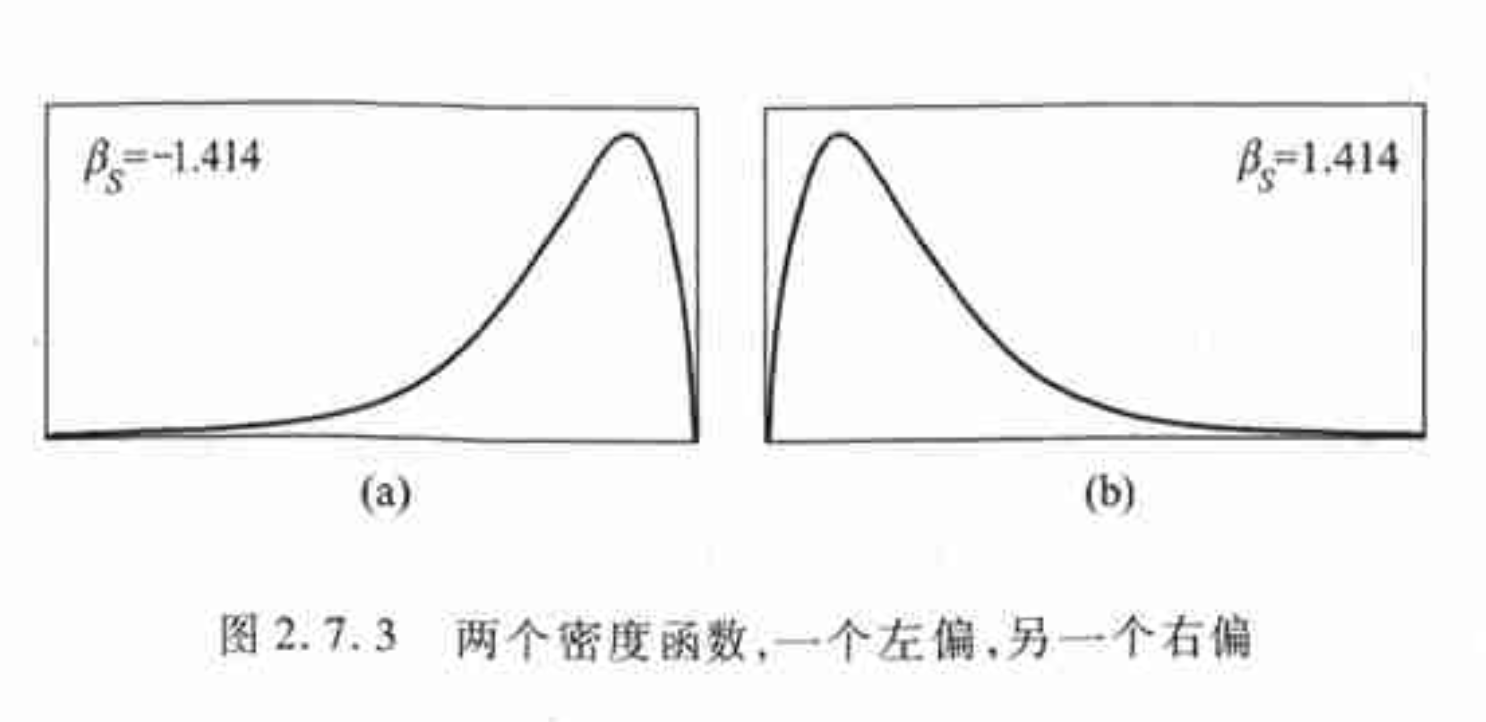
2.7.6 峰度系数

定义 设随机变量 $X$ 的前四阶矩存在，则如下比值减去3

$$\beta_k=\frac{\nu_4}{\nu_{2}^{2}}-3=\frac{E\{[X-E(X)]^4\}}{[Var(X)]^{2}}-3$$

称为此分布的峰度系数，简称峰度。