第二章 信息的表示和处理
2.1 信息的存储
ISO C99 1999
ISO C11 2011
2.1.1 十六进制表示法 Hexadecimal Notation
十六进制表示法以 0x 或 0X 开头
下图是 十六进制、十进制和二进制值对照表

A = 10 C=12 E=14
练习题 2.1
Perform the following number conversions:
A. 0x25B9D2 to binary
0010 0101 1011 1001 1101 0010
B. binary 1010 1110 0100 1001 to hexadecimal
0xAE49
C. 0xA8B3D to binary
1010 1000 1011 0011 1101
D. binary 11 0010 0010 1101 1001 0110 to hexadecimal
0x322D96
练习题 2.2
| n | $2^n$(decimal) | $2^n$(hexadecimal) |
|---|---|---|
| 5 | 32 | 0x20 |
| 23 | 8388608 | 0x800000 |
| 15 | 32768 | 0x8000 |
| 12 | 4096 | 0x1000 |
| 6 | 64 | 0x40 |
| 8 | 256 | 0x100 |
练习题 2.3
| decimal | binary | hexadecimal |
|---|---|---|
| 0 | 0000 0000 | 0x00 |
| 158 | 1001 1110 | 0x9E |
| 76 | 0100 1100 | 0x4C |
| 145 | 1001 0001 | 0x91 |
| 174 | 1010 1110 | 0xAE |
| 60 | 0011 1100 | 0x3C |
| 241 | 1111 0001 | 0xF1 |
练习题 2.4
Without converting the numbers to decimal or binary, try to solve the following arithmetic problems, giving the answers in hexadecimal. Hint: Just modify the methods you use for performing decimal addition and subtraction to use base 16.
A. 0x605c + 0x5 = 0x6061
B. 0x605c − 0x20 = 0x603c
C. 0x605c + 32 = 0x607c
D. 0x60fa − 0x605c = 0x9e
2.1.2 数据大小
每个计算机都有一个 字长,表示指针的大小,也可由此确定虚拟内存空间的大小。比如说,如果一个计算机的字长是 32 位,那么它的指针大小就是 4 字节,虚拟内存空间最大为 $2^{32}=4*2^{30}=4GB$
1 | gcc -m32 prog.c # 编译为 32 位程序 |
C语言中不同数据类型的通常大小
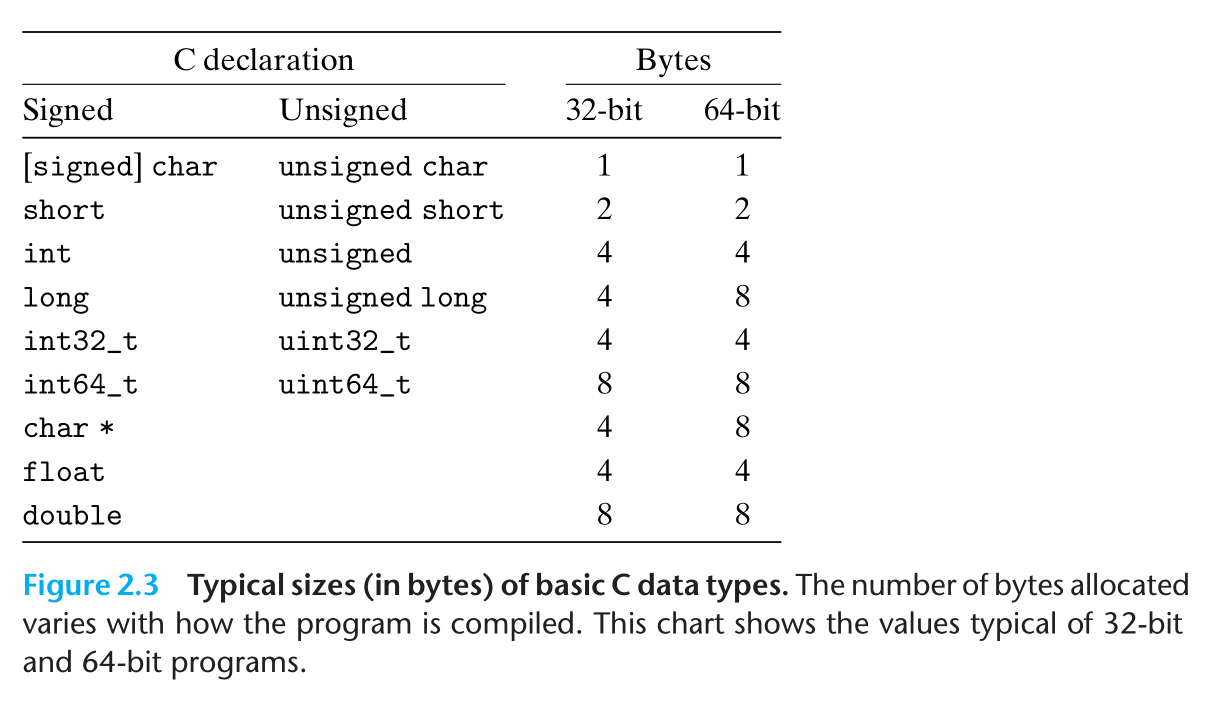
2.1.3 寻址和字节顺序
对于占用多个字节的程序对象,我们必须弄明白两件事情:此对象的地址是什么?它的各个字节在内存中是怎么排序的?
对于第一个问题,通常选择此对象整个字节序列中的最小地址作为此对象的地址
对于第二个问题,通常有两种方法:
现在假设一个 w 比特整型变量的比特表示是 $[x_{w-1},x_{w-2},…,x_1,x_0]$,其中 $x_{w-1}$ 称为最重要的位(the most significant bit)。假设 w 是8的倍数,那么这些位可以被分成一系列字节,最重要的字节是 $[x_{w-1},x_{w-2},…,x_{w-8}]$,最低的字节是 $[x_{7},x_{6},…,x_1,x_0]$ ,其它字节在这两个字节中间。
有些机器存储顺序是 从 最重要的字节 到 最不重要字节,这种存储方法称为 大端(big endian)
有些机器存储顺序相反, 称为 小端(little endian)
例如,存储 0x01234567 这个整型,大端的地址排列是这样的:

小端则相反,是这样的:

大多数 英特尔兼容机 是小端的,IBM的机器多是 大端的
[打印 字节序 的程序]
我用的 树莓派4B 也是小端的
练习题2.5
Consider the following three calls to show_bytes:
1 | int a = 0x12345678; |
Indicate the values that will be printed by each call on a little-endian machine and on a big-endian machine:
A. Little endian: 78 Big endian: 12
B. Little endian: 7856 Big endian: 1234
C. Little endian: 785634 Big endian: 123456
2.1.4 字符串的表示
在C中,字符串是以 null 结尾的字符序列
练习题 2.7
What would be printed as a result of the following call to show_bytes?
1 | const char *m = "mnopqr"; |
输出:6D6E6F707172
2.1.6 布尔代数 简介
C语言中的布尔代数:

练习题 2.8
Fill in the following table showing the results of evaluating Boolean operations on bit vectors.
| operation | result | |
|---|---|---|
| a | 01001110 | |
| b | 11100001 | |
| ~a | 10110001 | |
| ~b | 00011110 | |
| a & b | 01000000 | |
| a \ | b | 11101111 |
| a ^ b | 10101111 |
练习题 2.9
Computers generate color pictures on a video screen or liquid crystal display by mixing three different colors of light: red, green, and blue. Imagine a simple scheme, with three different lights, each of which can be turned on or off, projecting onto a glass screen:
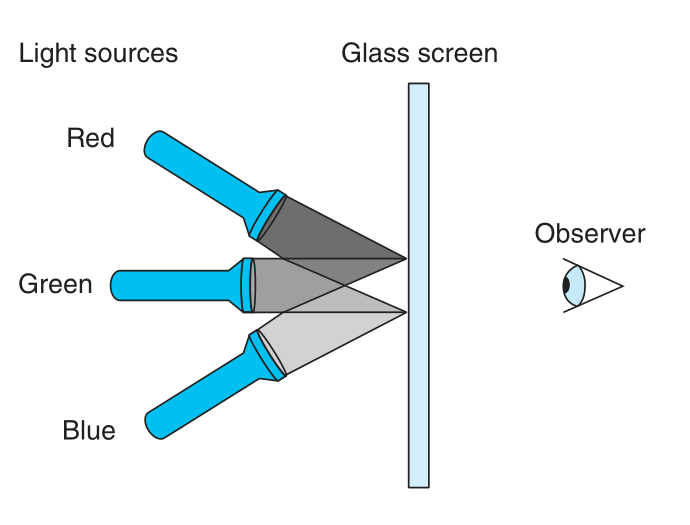
We can then create eight different colors based on the absence (0) or presence (1) of light sources R, G, and B:
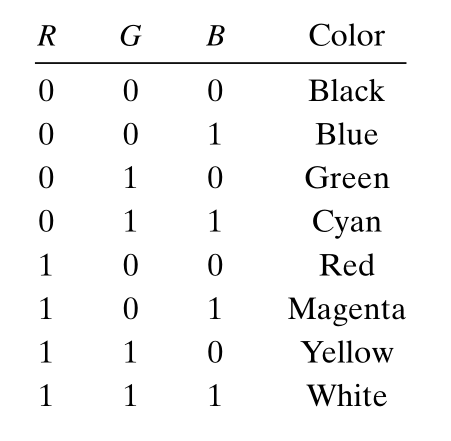
Each of these colors can be represented as a bit vector of length 3, and we can apply Boolean operations to them.
A. The complement of a color is formed by turning off the lights that are on and turning on the lights that are off. What would be the complement of each of the eight colors listed above?
Blue 111 & 001 000 |(001)
Green 111&010 000|(010)
B. Describe the effect of applying Boolean operations on the following colors:
Blue | Green = Cyan
Yellow & Cyan = Green
Red ^ Magenta = Blue
2.1.7 C语言中 的 位运算
C语言支持直接的位运算。
位运算的一个常见应用是执行 掩码运算(masking operations)
练习题 2.10
As an application of the property that a ^ a = 0 for any bit vector a, consider the following program:
1 | void inplace_swap(int *x, int *y) { |
Starting with values a and b in the locations pointed to by x and y, respectively, fill in the table that follows, giving the values stored at the two locations after each step of the procedure. Use the properties of ^ to show that the desired effect is achieved. Recall that every element is its own additive inverse (that is, a ^ a = 0).
| STEP | $*x$ | $*y$ |
|---|---|---|
| initially | a | b |
| step 1 | a | a^b |
| step2 | a^a^b=b | a^b |
| step3 | b | b^a^b=a |
练习题 2.12
Write C expressions, in terms of variable x, for the following values. Your code should work for any word size w ≥ 8. For reference, we show the result of evalu- ating the expressions for x = 0x87654321, with w = 32.
A. The least significant byte of x, with all other bits set to 0. [0x00000021]
x=x & 0x000000FF;
B. All but the least significant byte of x complemented, with the least significant byte left unchanged. [0x789ABC21]
x=x ^ 0xFFFFFF00;
C. The least significant byte set to all ones, and all other bytes of x left unchanged. [0x876543FF]
x=x | 0x000000FF;
练习题 2.13
The Digital Equipment VAX computer was a very popular machine from the late 1970s until the late 1980s. Rather than instructions for Boolean operations and and or, it had instructions bis (bit set) and bic (bit clear). Both instructions take a data word x and a mask word m. They generate a result z consisting of the bits of x modified according to the bits of m. With bis, the modification involves setting z to 1 at each bit position where m is 1. With bic, the modification involves setting z to 0 at each bit position where m is 1.
To see how these operations relate to the C bit-level operations, assume we have functions bis and bic implementing the bit set and bit clear operations, and that we want to use these to implement functions computing bitwise operations | and ^, without using any other C operations. Fill in the missing code below. Hint: Write C expressions for the operations bis and bic.
1 | /* Declarations of functions implementing operations bis and bic */ |
2.1.8 C语言中的逻辑运算
||、&&、!
练习题 2.14
Suppose that a and b have byte values 0x55 and 0x46, respectively. Fill in the following table indicating the byte values of the different C expressions:
| Expression | Value | Expression | Value | |||
|---|---|---|---|---|---|---|
| a & b | 0100 0100 | a && b | 0x01 | |||
| a\ | b | 0101 0111 | a\ | \ | b | 0x01 |
| ~a\ | ~b | 1011 1011 | !a \ | \ | !b | 0x00 |
| a & !b | 0000 0000 | a && ~b | 0x01 |
练习题 2.15
Using only bit-level and logical operations, write a C expression that is equivalent to x == y. In other words, it will return 1 when x and y are equal and 0 otherwise.
!(x^y)
2.1.9 C语言中的移位操作
即 左移操作符 << 和 右移操作符 >>
其中右移操作符有说法,总的来说,机器支持两种形式的右移操作:
逻辑右移:右移后产生的空位用 0 填充 $[0,…,0,x_{w−1},x_{w−2},…x_k]$
算术右移:右移后产生的空位用 最高位的值 填充 $[x_{w−1},…,x_{w−1},x_{w−1},x_{w−2},…x_k]$
C语言标准并没有明确规定使用哪种形式的右移。一般情况下,对于有符号数据使用 算术 右移;无符号数据 使用 逻辑 右移
练习题 2.16
Fill in the table below showing the effects of the different shift operations on single- byte quantities. The best way to think about shift operations is to work with binary representations. Convert the initial values to binary, perform the shifts, and then convert back to hexadecimal. Each of the answers should be 8 binary digits or 2 hexadecimal digits.
| Logical | Logical | Arithmetic | Arithmetic | ||||
|---|---|---|---|---|---|---|---|
| a | a | a<<2 | a<<2 | a>>3 | a>>3 | a>>3 | a>>3 |
| Hex | Binary | Binary | Hex | Binary | Hex | Binary | Hex |
| 0xd4 | 1101 0100 | 0101 0000 | 0x50 | 0001 1010 | 0x1a | 1111 1010 | 0xfa |
| 0x64 | 0110 0100 | 1001 0000 | 0x90 | 0000 1100 | 0x0c | 0000 1100 | 0x0c |
| 0x72 | 0111 0010 | 1100 1000 | 0xc8 | 0000 1110 | 0x0e | 0000 1110 | 0x0e |
| 0x44 | 0100 0100 | 0001 0000 | 0x10 | 0000 1000 | 0x08 | 0000 1000 | 0x08 |
2.2 整数的表示方法 Integer Representations
这一小节中要用到的一些运算的简称:
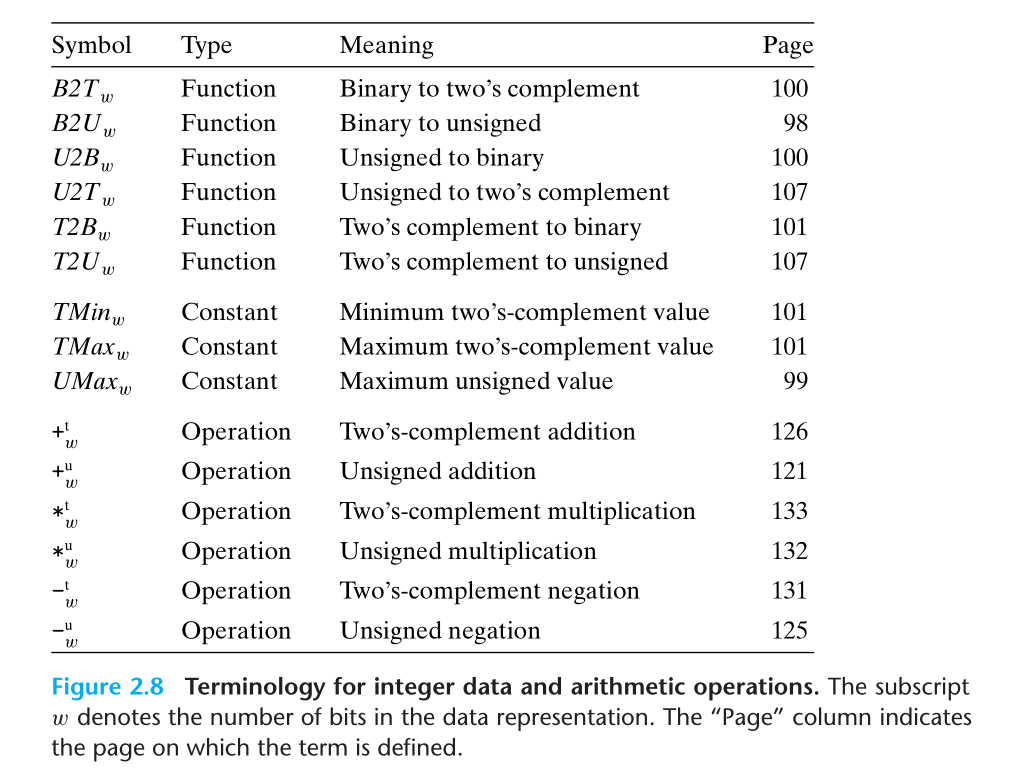
2.2.1 整数数据类型
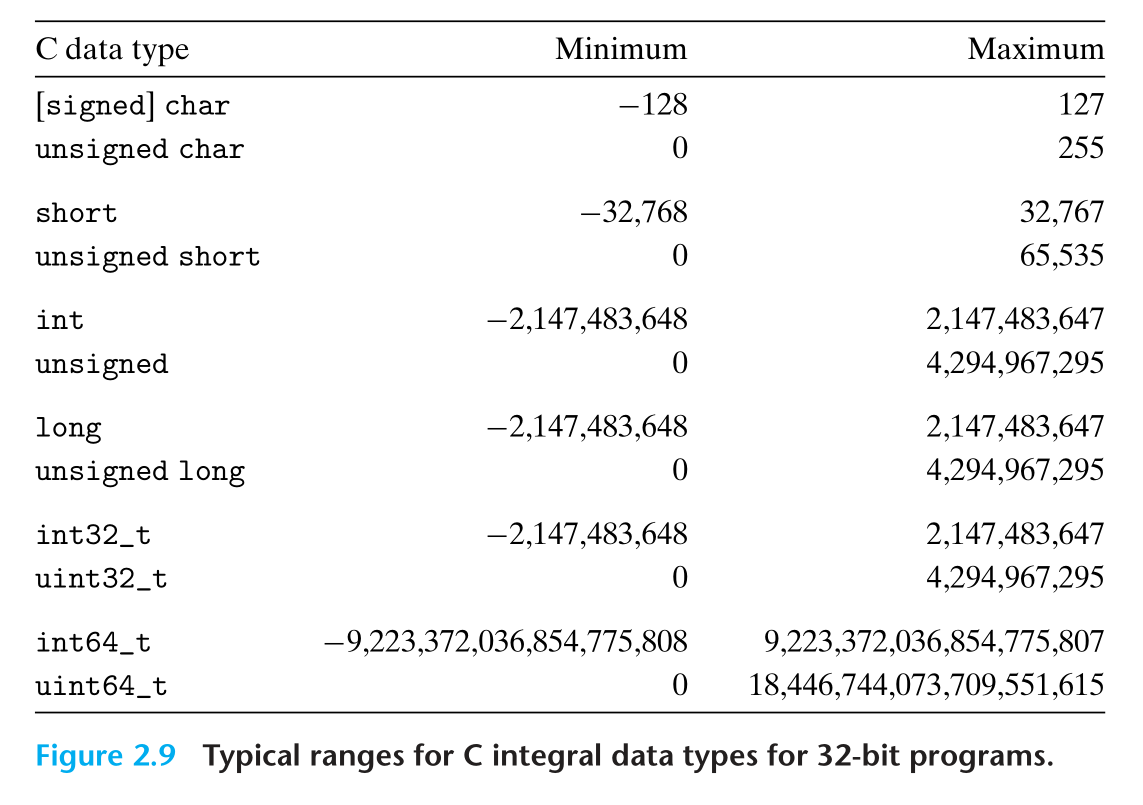
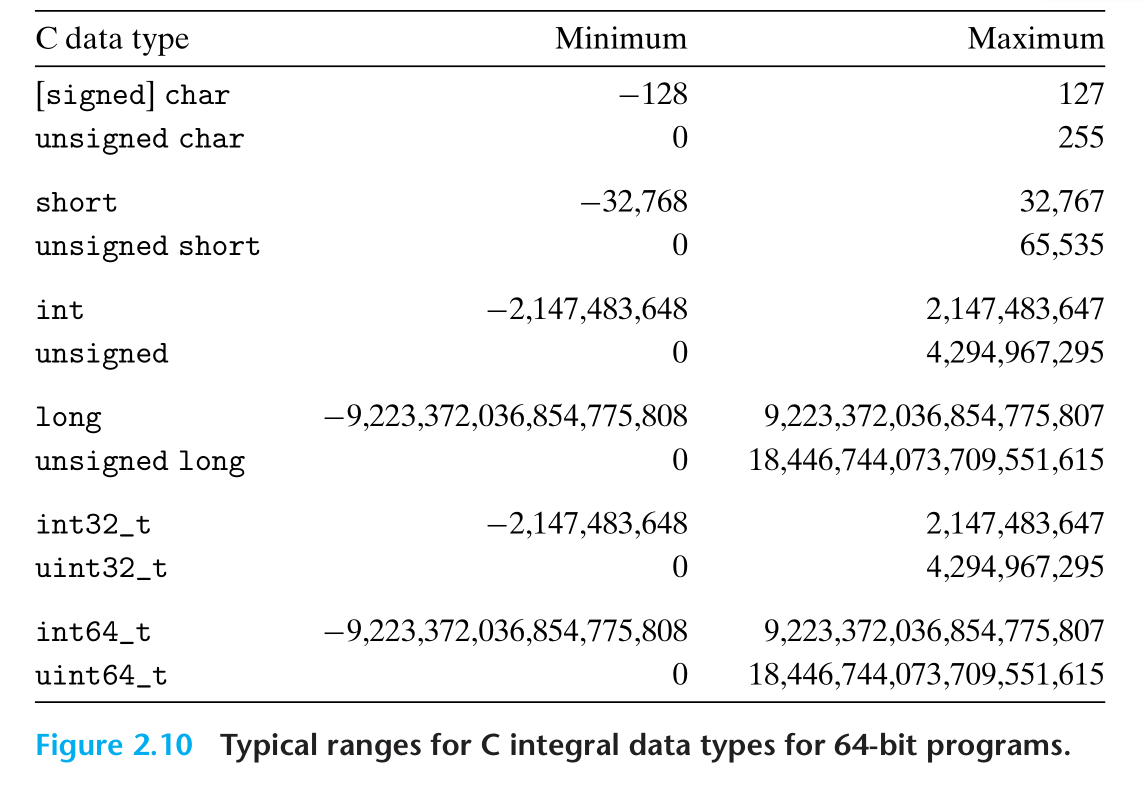
2.2.2 无符号类型的编码
现在考虑 一个 $w$ 位的整型数据。我们或者把它表示为位向量 $\vec{x}$ ,或者把它表示为 各个位的集合 $[x_{w−1},x_{w−2},…,x_0]$ 。现在可以定义函数 $B2U_w$ (for “binary to unsigned,” length w)
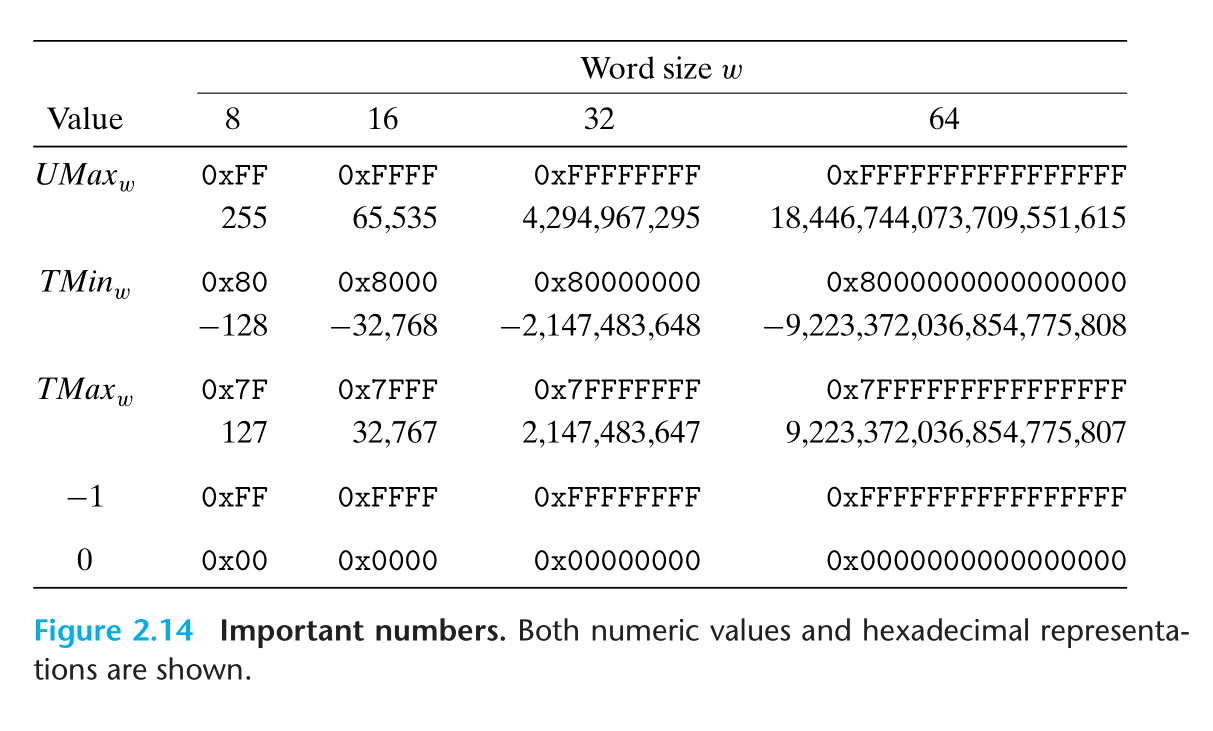
2.2.3 2的补码 Two’s-Complement Encodings
2的补码中,最重要的位具有 负 权重
现在可以定义 $B2T_w$ (for “binary to two’s complement” length w)
练习题 2.17
| $\vec{x}$ hexadecimal | $\vec{x}$ binary | $B2U_4(\vec{x})$ | $B2T_4(\vec{x})$ |
|---|---|---|---|
| 0xA | 1010 | 10 | -6 |
| 0x1 | 0001 | 1 | 1 |
| 0xB | 1011 | 11 | -5 |
| 0x2 | 0010 | 2 | 2 |
| 0x7 | 0111 | 7 | 7 |
| 0xC | 1100 | 12 | -4 |
练习题 2.18
In Chapter 3, we will look at listings generated by a disassembler, a program that converts an executable program file back to a more readable ASCII form. These files contain many hexadecimal numbers, typically representing values in two’s- complement form. Being able to recognize these numbers and understand their significance (for example, whether they are negative or positive) is an important skill.
For the lines labeled A–I (on the right) in the following listing, convert the hexadecimal values (in 32-bit two’s-complement form) shown to the right of the instruction names (sub, mov, and add) into their decimal equivalents:
1 | 4004d0: 48 81 ec e0 02 00 00 sub $0x2e0,%rsp A.0x2e0=736 |
2.2.4 有符号和无符号类型之间的转换
记住一个规则:在不同类型之间转换的时候,数据的位模式是不变的
练习题 2.19
| x | $T2U_4(X)$ |
|---|---|
| -1 | 15 |
| -5 | 11 |
| -6 | 10 |
| -4 | 12 |
| 1 | 1 |
| 8 |
2.2.5 C语言中的 有符号 和 无符号 类型
C语言中,有符号类型和无符号类型之间可以相互转换,这种转换在以下两种情况下发生:
显示类型转换:
1 | int tx, ty; |
隐式类型转换:
1 | int tx, ty; |
如果一个表达式中既有有符号类型,又有无符号类型,C语言会自动将有符号类型转换为无符号类型
练习题 2.21
| Expression | Type | Evaluation |
|---|---|---|
| -2147483647-1 == 2147483648U | unsigned | 1 |
| -2147483647-1 < 2147483647 | signed | 1 |
| -2147483647-1U < 2147483647 | unsigned | 0 |
| -2147483647-1 < -2147483647 | signed | 1 |
| -2147483647-1U < -2147483647 | unsigned | 1 |
2.2.6 扩展一个数的 位 表示
为什么要拓展一个数的位呢?
这在类型转换的时候要用到,比如从 short 转换成 int
对于无符号类型,执行 零扩展(zero extension)
对于有符号类型(采用2的补码),执行 符号扩展(sign extension)
练习题 2.23
Consider the following C functions:
1 | int fun1(unsigned word) { |
Assume these are executed as a 32-bit program on a machine that uses two’s- complement arithmetic. Assume also that right shifts of signed values are per- formed arithmetically, while right shifts of unsigned values are performed logically.
A. Fill in the following table showing the effect of these functions for several example arguments. You will find it more convenient to work with a hexadecimal representation. Just remember that hex digits 8 through F have their most significant bits equal to 1.
| w | fun1(w) | fun2(w) |
|---|---|---|
| 0x00000076 | 0x00000076 | 0x00000076 |
| 0x87654321 | 0x00000021 | 0x00000021 |
| 0x000000C9 | 0x000000C9 | 0xFFFFFFC9 |
| 0xEDCBA987 | 0x00000087 | 0xFFFFFF87 |
2.2.7 截断数字 Truncating Numbers
截断数字比扩展数字位数要简单粗暴得多:把要截断的位丢弃,仅此而已
练习题 2.24
| Hex | Hex | Unsigned | Unsigned | 2‘s complement | 2‘s complement |
|---|---|---|---|---|---|
| original | truncated | original | truncated | original | truncated |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 3 | 3 | 3 | 3 | 3 | 3 |
| 5 | 5 | 5 | 5 | 5 | -3 |
| C | 4 | 12 | 4 | -4 | -4 |
| E | 6 | 14 | 6 | -2 | -2 |
2.2.8 对于 有符号类型 和 无符号类型 的建议
练习题 2.25
Consider the following code that attempts to sum the elements of an array a, where the number of elements is given by parameter length:
1 | /* WARNING: This is buggy code */ |
When run with argument length equal to 0, this code should return 0.0. Instead, it encounters a memory error. Explain why this happens. Show how this code can be corrected.
length-1 = UMAX,所以这个循环不会跳出,而是会一直访问不存在的 a[i]
练习题 2.26
You are given the assignment of writing a function that determines whether one string is longer than another. You decide to make use of the string library function strlenhaving the following declaration:
1 | /* Prototype for library function strlen */ |
Here is your first attempt at the function:
1 | /* Determine whether string s is longer than string t */ |
When you test this on some sample data, things do not seem to work quite right. You investigate further and determine that, when compiled as a 32-bit program, data type size_t is defined (via typedef) in header file stdio.h to be unsigned.
A. For what cases will this function produce an incorrect result?
当 s 长度 短于 t 的长度时,strlen(s) - strlen(t) 会得到一个正数
B. Explain how this incorrect result comes about.
strlen 的返回值 size_t 是无符号整型,因此两个这样的值相减永远不会产生负数值,此函数也就不能正常工作
C. Show how to fix the code so that it will work reliably.
避免减法运算,将返回语句改成 return strlen(s) > strlen(t);
2.3 整数运算
2.3.1 无符号加法

如何检测 overflow ?
如果两个无符号整型的和小于 这两个整型中的任意一个,那么肯定发生了 溢出
练习题 2.27
Write a function with the following prototype:
1 | /* Determine whether arguments can be added without overflow */ |
This function should return 1 if arguments x and y can be added without causing overflow.
由无符号加法可以拓展到无符号减法
练习题 2.28
| x | x | $-_4^ux$ | $-_4^ux$ |
|---|---|---|---|
| Hex | Decimal | Decimal | Hex |
| 1 | 1 | 15 | F |
| 4 | 4 | 12 | C |
| 7 | 7 | 9 | 9 |
| A | 10 | 6 | 6 |
| E | 14 | 2 | 2 |
2.3.2 2的补码的加法
对于 $[-2^{w-1},2^{w-1}-1]$ 内的两个整型 $x,y$
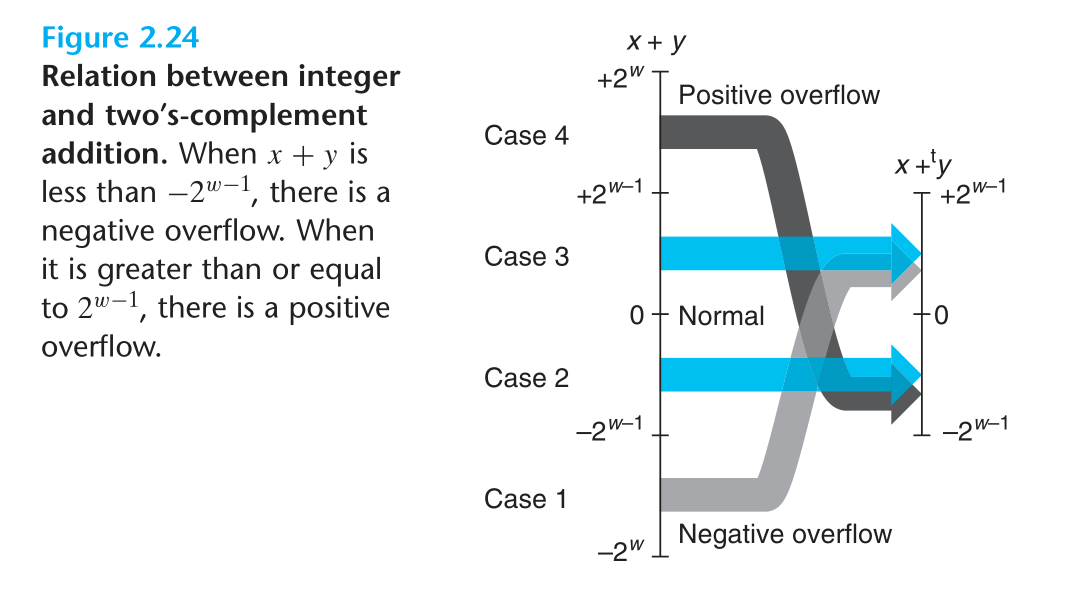
如何检测2的补码 overflow ?
对于在 $[TMin_w,TMax_w]$ 内的两个整型 $x,y$ ,令 $s\doteq x+_w^ty$
当且仅当 $x>0,y>0, but s\le 0$ 时,发生了正溢出
当且仅当 $x<0,y<0, but s\ge 0$ 时,发生了负溢出
练习题 2.29
| $x$ | $y$ | $x+y$ | $x+_5^ty$ | Case |
|---|---|---|---|---|
| -12 | -15 | -27 | 5 | 1 |
| [10100] | [10001] | [100101] | [00101] | |
| -8 | -8 | -16 | -16 | 2 |
| [11000] | [11000] | [110000] | [10000] | |
| -9 | 8 | -1 | -1 | 2 |
| [10111] | [01000] | [11111] | [11111] | |
| 2 | 5 | 7 | 7 | 3 |
| [00010] | [00101] | [00111] | [00111] | |
| 12 | 4 | 16 | -16 | 4 |
| [01100] | [00100] | [10000] | [10000] |
练习题 2.30
Write a function with the following prototype:
1 | /* Determine whether arguments can be added without overflow */ |
This function should return 1 if arguments x and y can be added without causing overflow.
练习题 2.31
Your coworker gets impatient with your analysis of the overflow conditions for two’s-complement addition and presents you with the following implementation of tadd_ok:
1 | /* Determine whether arguments can be added without overflow */ |
You look at the code and laugh. Explain why.
假如发生了正溢出,则 $sum=x+y-2^w$ , $sum-x=y-2^w=y$ 恒成立,同理,$sum-y == x$ 恒成立
练习题 2.32
You are assigned the task of writing code for a function tsub_ok, with arguments x and y, that will return 1 if computing x-y does not cause overflow. Having just written the code for Problem 2.30, you write the following:
1 | /* Determine whether arguments can be subtracted without overflow */ |
For what values of x and y will this function give incorrect results? Writing a correct version of this function is left as an exercise (Problem 2.74).
$y=TMin ,x=任一负数$
tadd_ok 判断结果是负溢出
而 x-y 结果是一个正数,不会溢出
2.3.3 2的补码的减法
练习题 2.33
| x | x | $-_4^t x$ | $-_4^t x$ |
|---|---|---|---|
| Hex | Decimal | Decimal | Hex |
| 2 | 2 | -2 | E |
| 3 | 3 | -3 | D |
| 9 | -7 | 7 | 7 |
| B | -5 | 5 | 5 |
| C | -4 | 4 | 4 |
2.3.4 无符号整型的乘法
2.3.5 2的补码的乘法
书中在这里特别提到,无符号和2的补码整型 在 相乘并截断后的位模式是一样的,也就是说:
并举了以下例子:

练习题 2.34
| Mode | x | x | y | y | $x\cdot y$ | $x\cdot y$ | Truncated $x\cdot y$ | Truncated $x\cdot y$ |
|---|---|---|---|---|---|---|---|---|
| Unsigned | 4 | [100] | 5 | [101] | 20 | [10100] | 4 | [100] |
| Two’s complement | -4 | [100] | -3 | [101] | 12 | [1100] | -4 | [100] |
| Unsigned | 2 | [010] | 7 | [111] | 14 | [1110] | 6 | [110] |
| Two’s complement | 2 | [010] | -1 | [111] | -2 | [1110] | -2 | [110] |
| Unsigned | 6 | [110] | 6 | [110] | 36 | [100100] | 4 | [100] |
| Two’s complement | -2 | [110] | -2 | [110] | 4 | [100] | -4 | [100] |
练习题 2.35
You are given the assignment to develop code for a function tmult_ok that will determine whether two arguments can be multiplied without causing overflow. Here is your solution:
1 | /* Determine whether arguments can be multiplied without overflow */ |
You test this code for a number of values of $x$ and $y$, and it seems to work properly. Your coworker challenges you, saying, “If I can’t use subtraction to test whether addition has overflowed (see Problem 2.31), then how can you use division to test whether multiplication has overflowed?”
Devise a mathematical justification of your approach, along the following lines. First, argue that the case $x = 0$ is handled correctly. Otherwise, consider w-bit numbers $x$ ($x \ne 0$), $y$, $p$, and $q$, where $p$ is the result of performing two’s- complement multiplication on $x$ and $y$, and $q$ is the result of dividing $p$ by $x$.
- Show that $x\cdot y$, the integer product of $x$ and $y$, can be written in the form $x \cdot y=p+t2^w$,where $t\ne 0$ if and only if the computation of $p$ overflows.
- Show that $p$ can be written in the form $p = x \cdot q + r$, where |$r| < |x|$.
- Show that $q = y$ if and only if $r = t = 0$.
练习题 2.36
For the case where data type int has 32 bits, devise a version of tmult_ok (Problem 2.35) that uses the 64-bit precision of data type int64_t, without using division.
1 | int tmult_ok(int x, int y) { |
练习题 2.37
You are given the task of patching the vulnerability in the XDR code below for the case where both data types int and size_t are 32 bits.
1 | /* Illustration of code vulnerability similar to that found in |
You decide to eliminate the possibility of the multiplication overflowing by computing the number of bytes to allocate using data type uint64_t. You replace the original call to malloc (line 10) as follows:
1 | uint64_t asize = ele_cnt * (uint64_t) ele_size; |
Recall that the argument to malloc has type size_t.
A. Does your code provide any improvement over the original?
没有任何改进,在调用 malloc 的时候,asize 还是会被隐式转换为 size_t 类型
B. How would you change the code to eliminate the vulnerability?
增加判断 ele_cnt * ele_size 是否会溢出的代码,如果会,则直接返回并给出错误信息
2.3.6 与常数相乘
无符号整型乘以 2 的幂
For C variables $x$ and $k$ with unsigned values $x$ and $k$, such that $0 ≤ k < w$, the C expression $x << k$ yields the value $x *_u^w 2^k$.
2的补码乘以 2 的幂
For C variables $x$ and $k$ with two’s-complement value $x$ and unsigned value $k$, such that $0 ≤ k < w$, the C expression $x << k$ yields the value $x *_t^w 2^k$.
练习题 2.38
As we will see in Chapter 3, the LEA instruction can perform computations of the form $(a<<k)+b$, where $k$ is either 0, 1, 2, or 3, and $b$ is either 0 or some program value. The compiler often uses this instruction to perform multiplications by constant factors. For example, we can compute $3*a$ as $(a<<1) + a$.
Considering cases where $b$ is either 0 or equal to $a$, and all possible values of $k$, what multiples of $a$ can be computed with a single LEA instruction?
$b=0$ 可以计算偶数倍
$b = a$ 可以计算奇数倍
所以理论上这个指令可以计算 $a$ 的任意倍数(实际结果要考虑溢出问题,但是溢出问题与这里讨论 LEA 指令的功能无关,因为就算不使用这条指令,计算倍数的时候也会发生溢出)
可以计算$2^k$倍数和$2^k+1$的倍数,也就是 1,2,3,4,5,8,9,16,17…
经过上面的讨论,现在考虑如何用 移位运算 和 加减运算 来代替 乘法运算。比如现在要计算 $x*K$ ,其中 $K$ 是常数,且其位模式为 $[(0…0)(1…1)(0…0)…(1…1)]$
以 $K=14$ 为例,其位模式为 $[1110]$ 。对于位模式中连续出现的 $1$ ,记其最高位数 为 $n$ (此处 $n=3$),最低位数为 $m$ (此处 $m=1$)
有两种方法能够完成替代工作:
A: $(x<<n)+(x<<(n−1))+…+(x<<m)$
B: $(x<<(n+1))-(x<<m)$
练习题 2.40
For each of the following values of $K$, find ways to express $x*K$ using only the specified number of operations, where we consider both additions and subtractions to have comparable cost. You may need to use some tricks beyond the simple form A and B rules we have considered so far.
| $K$ | Shifts | Add/Subs | Expression |
|---|---|---|---|
| 7 | 1 | 1 | $(x<<3)-x$ |
| 30 | 4 | 3 | $(x<<4)+(x<<3)+(x<<2)+(x<<1)$ |
| 28 | 2 | 1 | $(x<<5)-(x<<2)$ |
| 55 | 2 | 2 | $(x<<6)-(x<<3)-x$ |
练习题 2.41
For a run of ones starting at bit position $n$ down to bit position $m$ ($n ≥ m$), we saw that we can generate two forms of code, A and B. How should the compiler decide which form to use?
2.3.7 整型除以 2 的幂
同样的,除法也可以用 移位 和 加减 操作来代替。不同的是,此时的移位操作变成了 右移,自然地就要涉及到 无符号整型的逻辑右移 和 2的补码的 算术右移
书中在这里强调了:对于整型除法的结果,正数向下取整;负数向上取整;
也就是说,For $x ≥ 0$ and $y > 0$, integer division should yield $⌊x/y⌋$, while for $x < 0$ and $y > 0$, it should yield $⌈x/y⌉$.
即取整后的结果都更靠近 0 了(round toward zero)
无符号整型除以 2 的幂非常直接,因为 无符号整型总是采用逻辑右移
For C variables $x$ and $k$ with unsigned values $x$ and $k$, such that $0 ≤ k < w$, the C expression $x >> k$ yields the value $⌊x/2k⌋$.
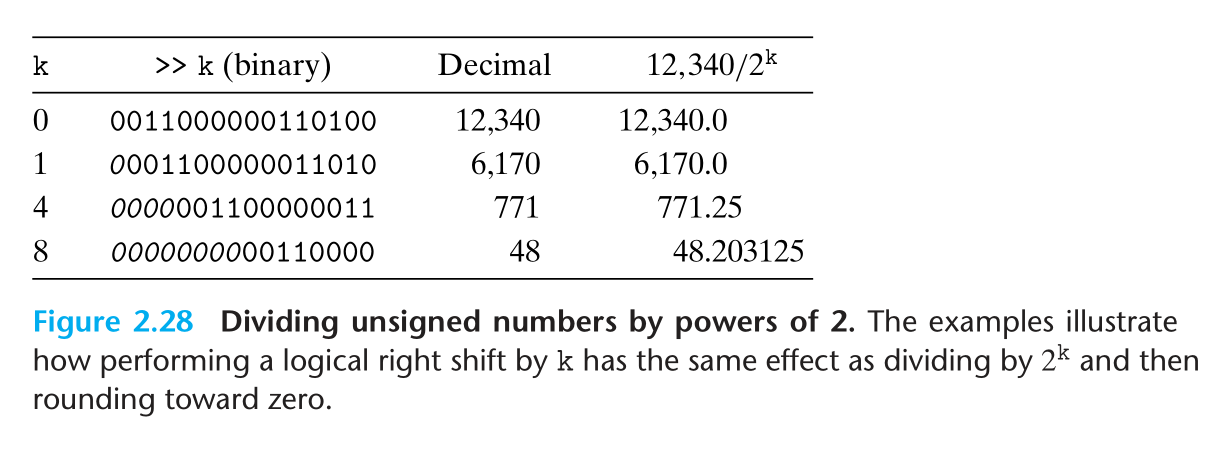
2的补码 除以 2 的幂则要复杂一些,首先是采用算术右移
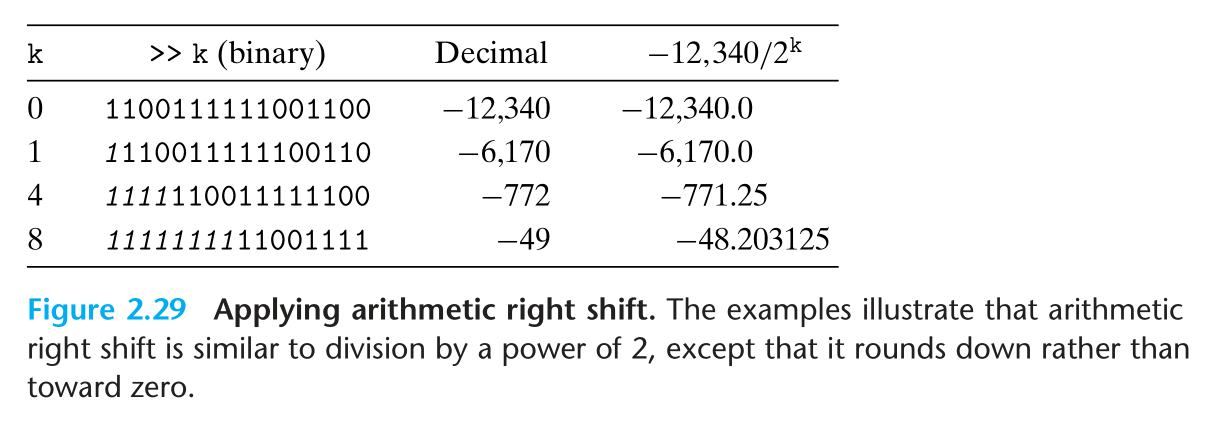
但是从表中可以看到,最终的结果是 向下取整 而不是 向上取整 ,我们必须对这个策略做一些改进
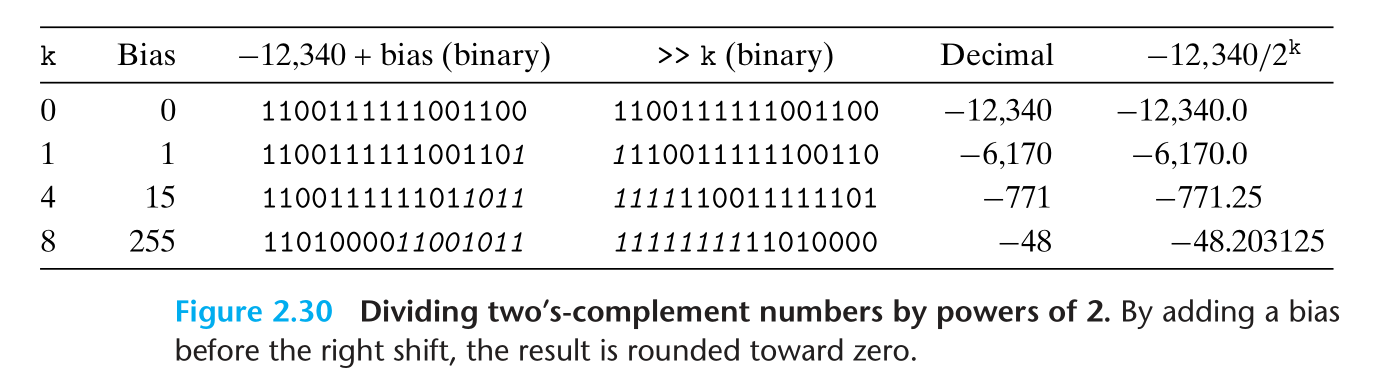
利用 $⌈x/y⌉ = ⌊(x+y−1)/y⌋$ 这一性质,我们在执行除法运算之前,给 $x$ 加上 $2^k-1$ 即可,即 $⌈x/2k⌉=(x+(1<
练习题 2.42
Write a function div16 that returns the value x/16 for integer argument x. Your function should not use division, modulus, multiplication, any conditionals (if or ?:), any comparison operators (e.g., <, >, or ==), or any loops. You may assume that data type int is 32 bits long and uses a two’s-complement representation, and that right shifts are performed arithmetically.
1 | int div16(int x){ |
练习题 2.43
In the following code, we have omitted the definitions of constants M and N:
1 |
|
We compiled this code for particular values of M and N. The compiler optimized the multiplication and division using the methods we have discussed. The following is a translation of the generated machine code back into C:
1 | /* Translation of assembly code for arith */ |
What are the values of M and N?
M=31 ,N=8
2.3.8 关于整数运算的 Final Thoughts
练习题 2.44
Assume data type int is 32 bits long and uses a two’s-complement representation for signed values. Right shifts are performed arithmetically for signed values and logically for unsigned values. The variables are declared and initialized as follows:
1 | int x = foo(); /* Arbitrary value */ |
For each of the following C expressions, either (1) argue that it is true (evaluates to 1) for all values of x and y, or (2) give values of x and y for which it is false (evaluates to 0):
A. $(x > 0) || (x-1 < 0)$
$x=TMin_{32}=0x80000000=-2147483648<0$ 时,$x-1=TMax_{32}=0x7fffffff=2147483647>0$
B. $(x\&7) != 7||(x<<29 < 0)$
总是正确的
C. $(x * x) >= 0$
??貌似总是正确的
错的,x=65535(0xFFFF) 时,x*x = -131071(0xFFFE0001)
D. $x < 0 || -x <= 0$
总是正确的
E. $x > 0 || -x >= 0$
$x=TMin_{32}<0$ 时,$-x=TMin_{32}<0$
F. $x+y == uy+ux$
总是正确的,因为 $x+y$ 和 $uy+ux$ 的位模式都是一样,而在最后 $==$ 判断的时候 $x+y$ 又会被自动转换为无符号类型,所以判断结果总是 1
G. $x\sim y + uyux == -x$
总是正确的
2.4 浮点 Floating Point
2.4.1 二进制分数
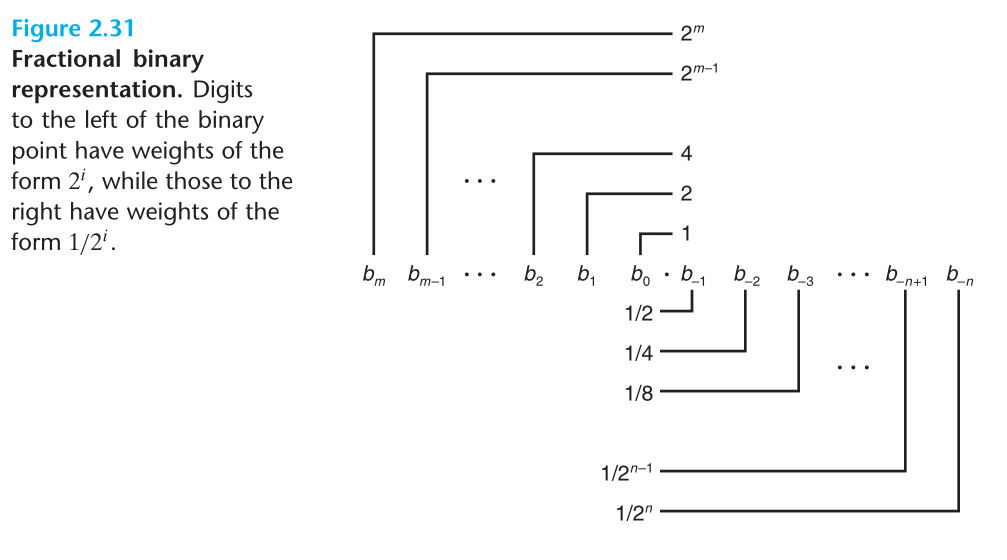
考虑下面这样的位模式
这样的位模式表示的数 $b$ 定义为
练习题 2.45
| Fractional value | Binary representation | Decimal representation |
|---|---|---|
| $\frac{1}{8}$ | 0.001 | 0.125 |
| $\frac{3}{4}$ | 0.11 | 0.75 |
| $\frac{5}{16}$ | 0.0101 | 0.3125 |
| $\frac{43}{16}$ | 10.1011 | 2.6875 |
| $\frac{9}{8}$ | 1.001 | 1.125 |
| $\frac{47}{8}$ | 101.111 | 5.875 |
| $\frac{51}{16}$ | 11.0011 | 3.1875 |
2.4.2 IEEE 浮点表示方法
IEEE 标准以 $V=(-1)^s\times M \times 2^E$ 的形式表示浮点数
- $s$ 是符号位,1 表示负数,0表示正数
- $M$ 是有效数字,它是一个二进制小数,处在 $[1,2)$ 或 $[0,1)$ 范围内
- $E$ 是指数
类似于十进制里使用的科学计数法
根据这个表示方法,可以把浮点的位表示分为三部分:
- $s$ 单独占一位以指示符号
- 分配 $k$ 比特表示指数 $E$
- 分配 $n$ 比特表示有效数字 $M$
位分配情况示意图:

根据指数部分的位模式,可以将浮点值分为以下几类
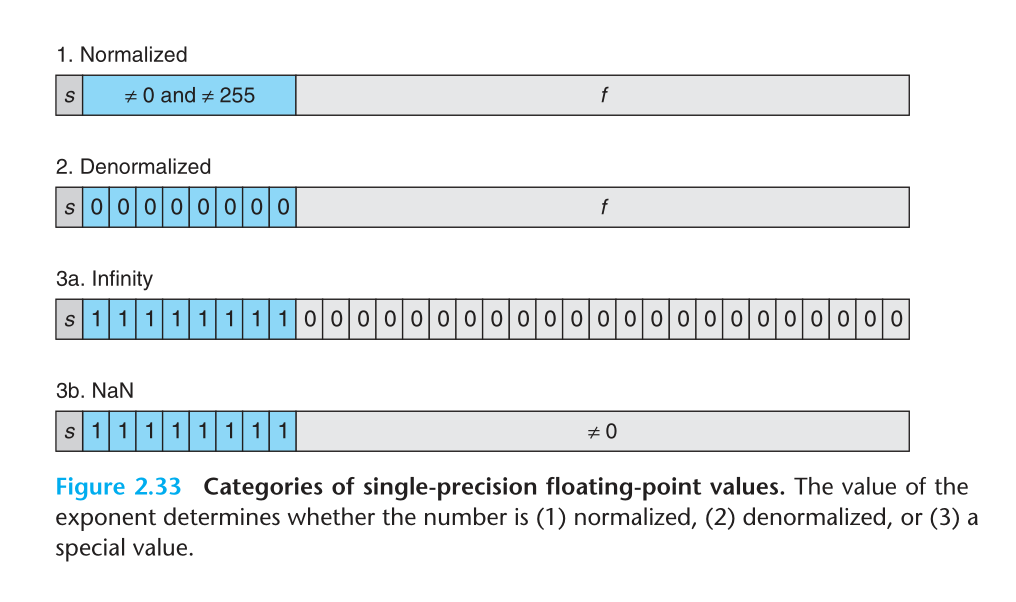
第一种 规范化的值
当 指数部分 的位模式 既非全 0 ,也非全 1 时表示的值称为规范化的值
此时 $E=e-Bias$ ,$e$ 就是位模式 $e_{k-1}\cdot \cdot\cdot e_1e_0$ 表示的无符号整型值,$Bias=2^{k-1}-1$
而有效数字位部分的值用 $f$ 表示($0\le f <1$),即 $f=0.f_{n-1}\cdot\cdot\cdot f_1f_0$ , 但是,有效数字 $M=1+f$
第二种 不规范的值
当 指数部分 的位模式 全是 0 时的值称为不规范的值
此时 $E=1-Bias$ , $M=f$
这可以用来表示绝对值很小的值
第三种 特殊值
指数部分全部为 1 是用来表示特殊值的(看 2.33 图)
$+\infty , -\infty , NaN$
2.4.3 举一些数作为例子
练习题 2.47
Consider a 5-bit floating-point representation based on the IEEE floating-point format, with one sign bit, two exponent bits ($k = 2$), and two fraction bits ($n = 2$). The exponent bias is $2^{2−1} − 1 = 1$.
The table that follows enumerates the entire nonnegative range for this 5-bit floating-point representation. Fill in the blank table entries using the following directions:
$e$ : The value represented by considering the exponent field to be an unsigned integer
$E$ : The value of the exponent after biasing
$2^E$ : The numeric weight of the exponent
$f$ : The value of the fraction
$M$ : The value of the significand
$2^E \times M$ : The (unreduced) fractional value of the number
$V$ : The reduced fractional value of the number
Decimal: The decimal representation of the number
| Bits | $e$ | $E$ | $2^E$ | $f$ | $M$ | $2^E \times M$ | $V$ | Decimal |
|---|---|---|---|---|---|---|---|---|
| 0 00 00 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 00 01 | 0 | 0 | 1 | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{4}$ | 0.25 |
| 0 00 10 | 0 | 0 | 1 | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | 0.5 |
| 0 00 11 | 0 | 0 | 1 | $\frac{3}{4}$ | $\frac{3}{4}$ | $\frac{3}{4}$ | $\frac{3}{4}$ | 0.75 |
| 0 01 00 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 01 01 | 1 | 0 | 1 | $\frac{1}{4}$ | $\frac{5}{4}$ | $\frac{5}{4}$ | $\frac{5}{4}$ | 1.25 |
| 0 01 10 | 1 | 0 | 1 | $\frac{1}{2}$ | $\frac{3}{2}$ | $\frac{3}{2}$ | $\frac{3}{2}$ | 1.5 |
| 0 01 11 | 1 | 0 | 1 | $\frac{3}{4}$ | $\frac{7}{4}$ | $\frac{7}{4}$ | $\frac{7}{4}$ | 1.75 |
| 0 10 00 | 2 | 1 | 2 | 0 | 1 | 2 | 2 | 2 |
| 0 10 01 | 2 | 1 | 2 | $\frac{1}{4}$ | $\frac{5}{4}$ | $\frac{5}{2}$ | $\frac{5}{2}$ | 2.5 |
| 0 10 10 | 2 | 1 | 2 | $\frac{1}{2}$ | $\frac{3}{2}$ | 3 | 3 | 3 |
| 0 10 11 | 2 | 1 | 2 | $\frac{3}{4}$ | $\frac{7}{4}$ | $\frac{7}{2}$ | $\frac{7}{2}$ | 3.5 |
| 0 11 00 | $+\infin$ | |||||||
| 0 11 01 | $NaN$ | |||||||
| 0 11 10 | $NaN$ | |||||||
| 0 11 11 | $NaN$ |
练习题 2.48
As mentioned in Problem 2.6, the integer 3,510,593 has hexadecimal representation 0x00359141, while the single-precision floating-point number 3,510,593.0 has hexadecimal representation 0x4A564504. Derive this floating-point representation and explain the correlation between the bits of the integer and floating-point representations.
$0x00359141=0000 0000 0011 0101 1001 0001 0100 0001 = 1.1 0101 1001 0001 0100 0001_2 \times 2^{21}$
$f=0.1 0101 1001 0001 0100 0001$
$e=21+2^{8-1}-1=2^7+2^4+2^2=10010100$
所以 3,510,593.0 的位模式
$0 10010100 101011001000101000001 = 0100 1010 0101 0110 0100 0101 0000 0100 = 0x4A564504$
练习题 2.49
A. For a floating-point format with an n-bit fraction, give a formula for the smallest positive integer that cannot be represented exactly (because it would require an $(n + 1)$-bit fraction to be exact). Assume the exponent field size $k$ is large enough that the range of representable exponents does not provide a limitation for this problem.
$2^{n+1}+1$
B. What is the numeric value of this integer for single-precision format ($n = 23$)?
$2^{24}+1$
2.4.4 四舍五入 Rounding
IEEE定义了4中不同的四舍五入模式 rounding modes
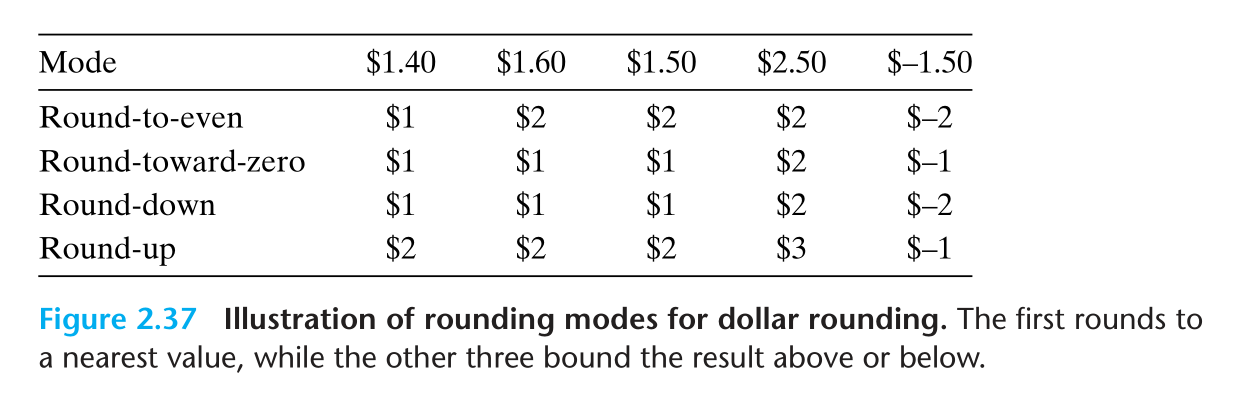
后三种都是一目了然的,只有第一种有些疑问
Round-to-even 模式采用这样的方式进行四舍五入:对于处在两个可能结果正中间的数,它保证舍入结果最后一位是偶数,所以 1.50 和 2.50 都被舍入为 2
练习题 2.50
Show how the following binary fractional values would be rounded to the nearest half (1 bit to the right of the binary point), according to the round-to-even rule. In each case, show the numeric values, both before and after rounding.
A. $10.111_2$
$11.0_2$
B. $11.010_2$
$11.0_2$
C. $11.000_2$
$11.0_2$
D. $10.110_2$
$11.0_2$
练习题 2.52
Consider the following two 7-bit floating-point representations based on the IEEE floating-point format. Neither has a sign bit—they can only represent nonnegative numbers.
Format A
- There are k = 3 exponent bits. The exponent bias is 3.
- There are n = 4 fraction bits.
Format B
- There are k = 4 exponent bits. The exponent bias is 7.
- There are n = 3 fraction bits.
Below, you are given some bit patterns in format A, and your task is to convert them to the closest value in format B. If necessary, you should apply the round-to- even rounding rule. In addition, give the values of numbers given by the format A and format B bit patterns. Give these as whole numbers (e.g., 17) or as fractions (e.g., 17/64).
| Format A | Format A | Format B | Format B |
|---|---|---|---|
| Bits | Value | Bits | Value |
| 011 0000 | 1 | 0111 000 | 1 |
| 101 1110 | $\frac{15}{2}$ | 1001 111 | $\frac{15}{2}$ |
| 010 1001 | $\frac{25}{32}$ | 0110 100 | $\frac{3}{4}$ |
| 110 1111 | $\frac{31}{2}$ | 1011 000 | 16 |
| 000 0001 | $\frac{1}{64}$ | 0001 000 | $\frac{1}{64}$ |
2.4.5 浮点运算
注意,由于浮点类型的表示方法,浮点运算满足交换律,但不满足结合律
monotonicity 单调性
2.4.6 C语言中的浮点
float double
练习题 2.53
Fill in the following macro definitions to generate the double-precision values $+∞$, $−∞$, and $−0$:
1 |
在 int ,float 和 double 类型之间转换的时候遵循以下规则(假设 int 是 32 位)
- 从
int到float,不能发生溢出,但是可能四舍五入(?) - 从
int或float到double,所有数字都可以平稳转换,因为double的表示范围包括了前两个类型的范围 - 从
double到float,可能溢出或四舍五入 - 从
float或double到int,会向 0 发生四舍五入
练习题 2.54
Assume variables x, f, and d are of type int, float, and double, respectively. Their values are arbitrary, except that neither f nor d equals $+∞$, $−∞$, or $NaN$. For each of the following C expressions, either argue that it will always be true (i.e., evaluate to 1) or give a value for the variables such that it is not true (i.e., evaluates to 0).
A. $x == (int)(double) x$
总是正确的
B. $x == (int)(float) x$
$x=TMax$
C. $d == (double)(float) d$
$d=1e40$ 时,右边是 $+\infin$
D. $f == (float)(double) f$
总是正确的
E. $f == -(-f)$
总是正确的
F. $1.0/2 == 1/2.0$
总是正确的
G. $d*d >= 0.0$
总是正确的
H. $(f+d)-f == d$
不对, $f=1e20,d=1.0$
